Question

【題目】【定義】已知P為△ABC所在平面內一點，連接PA，PB，PC，在△PAB，△PBC和△PAC中，若存在一個三角形與△ABC相似（全等除外），那么就稱P為△ABC的“共相似點”，根據“共相似點”是否落在三角形的內部，邊上或外部，可將其分為“內共相似點”，“邊共相似點”或“外共相似點”．
（1）據定義可知，等邊三角形（填“存在”或“不存在”）共相似點．
（2）如圖1，若△ABC的一個邊共相似點P與其對角頂點B的連線，將△ABC分割成的兩個三角形恰與原三角形均相似，試判斷△ABC的形狀，并說明理由．

（3）如圖2，在△ABC中，∠A＜∠B＜∠C，高線CD與角平分線BE交于點P，若P是△ABC的一個內共相似點，試說明點E是△ABC的邊共相似點，并直接寫出∠A的度數．

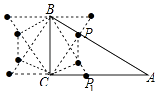
（4）如圖3，在Rt△ABC中，∠C=90°，∠A=30°，BC= ，若△PBC與△ABC相似，則滿足條件的P點共有個，順次連接所有滿足條件的P點而圍成的多邊形的周長為 ．

Answer 1

【答案】
（1）不存在
（2）

解：△ABC是直角三角形，理由如下：

根據題意得：△ABP∽△ACB，

∴∠ABP=∠C，

同理得：∠CBP=∠A，

∴∠ABC=∠A+∠C=180°﹣∠ABC，

解得：∠ABC=90°，

∴△ABC是直角三角形；

（3）

解：根據題意得：△PBC∽△CAB，

∴∠PBC=∠A，∠PCB=∠ABC，

∵BE平分∠ABC，

∴∠ABE=∠PBC，

∴∠A=∠ABE=∠PBC，

∴∠PCB=∠ABC=2∠A=2∠PBC，

∵∠BCE=∠ACB，∠PBC=∠A，

∴△BEC∽△ABC，

∴點E是△ABC的邊共相似點；

∵CD是△ABC的高，

∴∠CDB=90°，

∴∠PCB+∠ABC=90°，

∴2∠A+2∠A=90°，

解得：∠A=22.5°；

（4）8；6+
【解析】解：（1）根據“共相似點”的定義得：等邊三角形不存在共相似點．
所以答案是：不存在；
4）作CP⊥AB于P，則P為△ABC的“共相似點”；
過B作BC的垂線與CP的延長線的交點是△ABC的“共相似點”；
作∠ABC的平分線與AC的交點P1是△ABC的“共相似點”；
過C作BP1的垂線，垂足是△ABC的“共相似點”；
同理：以上四個△ABC的“共相似點”關于直線BC的對稱點是△ABC的“共相似點”；
∴△ABC的“共相似點”共有8個，如圖所示：
根據等邊三角形的性質和直角三角形的性質得：順次連接所有滿足條件的P點而圍成的多邊形的周長為 2×2+4× +2× =6+ ；
所以答案是：8；6+ ．

【考點精析】解答此題的關鍵在于理解相似三角形的性質的相關知識，掌握對應角相等，對應邊成比例的兩個三角形叫做相似三角形．