
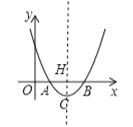
【題目】如圖,已知拋物線y=x2﹣4x+3與x軸交于A,B兩點,其頂點為C.
(1)對于任意實數m,點M(m,﹣2)是否在該拋物線上?請說明理由;
(2)求證:△ABC是等腰直角三角形;
(3)若點D在x軸上,則在拋物線上是否存在點P,使得PD∥BC,且PD=BC?若存在,求點P的坐標;若不存在,請說明理由.

【答案】(1)不在;(2)答案見解析;(3)(![]() ,1)或(
,1)或(![]() ,1).
,1).
【解析】試題分析:(1)假如點M(m,﹣2)在該拋物線上,則﹣2=m2﹣4m+3,通過變形為:m2﹣4m+5=0,由根的判別式就可以得出結論;
(2)如圖,根據拋物線的解析式求出點C的坐標,再利用勾股定理求出AB、AC和BC的值,由勾股定理的逆定理就可以得出結論.
(3)假設存在點P,根據對角線互相平分的四邊形是平行四邊形,因此連接點P與點C的線段應被x軸平分,就可以求得P點的縱坐標為1,代入拋物線的解析式就可以求出P點的橫坐標.
試題解析:解:(1)假如點M(m,﹣2)在該拋物線上,∴﹣2=m2﹣4m+3,∴m2﹣4m+5=0,∴△=(﹣4)2﹣4×1×5=﹣4<0,∴此方程無實數解,∴點M(m,﹣2)不會在該拋物線上;
(2)過點C作CH⊥x軸,交x軸與點H,連接CA、CB.如圖,當y=0時,x2﹣4x+3=0,x1=1,x2=3.∵點A在點B左側,∴A(1,0),B(3,0),∴OA=1,OB=3,∴AB=2.
∵y=x2﹣4x+3,∴y=(x﹣2)2﹣1,∴C(2,﹣1),∴AH=BH=CH=1.
在Rt△AHC和Rt△BHC中,由勾股定理得,AC=![]() ,BC=
,BC=![]() ,∴AC2+BC2=AB2,∴△ABC是等腰直角三角形;
,∴AC2+BC2=AB2,∴△ABC是等腰直角三角形;
(3)存在這樣的點P.
∵PD∥BC,PD=BC,∴四邊形PBCD是平行四邊形,∴根據對角線互相平分的四邊形是平行四邊形,因此連接點P與點C的線段應被x軸平分,∴點P的縱坐標是1.∵點P在拋物線y=x2﹣4x+3上,∴x2﹣4x+3=1,解得x1=2﹣![]() ,x2=2+
,x2=2+![]() ,∴點P的坐標是(2﹣
,∴點P的坐標是(2﹣![]() ,1)或(2+
,1)或(2+![]() ,1).
,1).


科目:初中數學 來源: 題型:
【題目】如圖 1,AB∥CD,點 E 在 AB 上,點 M 在 CD 上,點 F 在直線 AB,CD 之間,連接 EF、FM, EF⊥FM,∠CMF=140°.
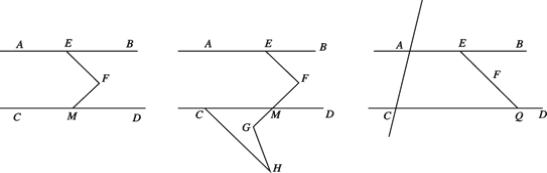
圖 1 圖 2 圖 3
(1)直接寫出∠AEF 的度數為 ________;
(2)如圖 2,延長 FM 到 G,點 H 在 FG 的下方,連接 GH,CH,若∠FGH=∠H+90°, 求∠MCH 的度數;
(3)如圖 3,作直線 AC,延長 EF 交 CD 于點 Q,P 為直線 AC 上一動點,探究∠PEQ,∠PQC 和∠EPQ 的數量關系,請直接給出結論.(題中所有角都是大于 0°小于 180°的角)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某水果批發商場經銷一種高檔水果,若每千克盈利10元,每天可售出500千克.經市場調查發現,在進貨價不變的情況下,若每千克漲價1元,日銷售量將減少20千克.現該商場要保證每天盈利6000元,同時又要使顧客得到實惠,求:
(1)每千克應漲價多少元?
(2)該水果月銷售(按每月30天)是多少千克?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x的一元二次方程x2-2![]() x+m=0有兩個不相等的實數根.
x+m=0有兩個不相等的實數根.
(1)求實數m的最大整數值;
(2)在(1)的條件下,方程的實數根是x1,x2,求代數式![]() +
+![]() -
-![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
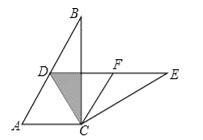
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠B=30°,將△ABC繞點C按照順時針方向旋轉m度后得到△DEC,點D剛好落在AB邊上.
(1)求m的值;
(2)若F是DE的中點,判斷四邊形ACFD的形狀,并說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
對于多項式![]() ,如果我們把
,如果我們把![]() 代入此多項式,發現
代入此多項式,發現![]() 的值為0,這時可以確定多項式中有因式
的值為0,這時可以確定多項式中有因式![]() :同理,可以確定多項式中有另一個因式
:同理,可以確定多項式中有另一個因式![]() ,于是我們可以得到:
,于是我們可以得到:![]() .
.
又如:對于多項式![]() ,發現當
,發現當![]() 時,
時,![]() 的值為0,則多項式
的值為0,則多項式![]() 有一個因式
有一個因式![]() ,我們可以設
,我們可以設![]() ,解得
,解得![]() ,
,![]() ,于是我們可以得到:
,于是我們可以得到:![]() .
.
請你根據以上材料,解答以下問題:
(1)當![]() 時,多項式
時,多項式![]() 的值為0,所以多項式
的值為0,所以多項式![]() 有因式 ,從而因式分解
有因式 ,從而因式分解![]() .
.
(2)以上這種因式分解的方法叫試根法,常用來分解一些比較復雜的多項式.請你嘗試用試根法分解多項式:①![]() ;②
;②![]() .
.
(3)小聰用試根法成功解決了以上多項式的因式分解,于是他猜想:
代數式![]() 有因式 , , ,
有因式 , , ,
所以分解因式![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AD為∠BAC的平分線,BM⊥AD,垂足為M,且AB=5,BM=2,AC=9,則∠ABC與∠C的關系為( )

A.∠ABC=2∠CB.∠ABC=![]() ∠CC.
∠CC.![]() ∠ABC=∠CD.∠ABC=3∠C
∠ABC=∠CD.∠ABC=3∠C
查看答案和解析>>
科目:初中數學 來源: 題型:
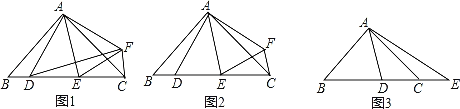
【題目】在△ABC中,AB=AC,∠BAC=2∠DAE=2α.
(1)如圖1,若點D關于直線AE的對稱點為F,求證:△ADF∽△ABC;
(2)如圖2,在(1)的條件下,若α=45°,求證:DE2=BD2+CE2;
(3)如圖3,若α=45°,點E在BC的延長線上,則等式DE2=BD2+CE2還能成立嗎?請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】知識是用來為人類服務的,我們應該把它們用于有意義的方面.下面就兩個情景請你作出評判.
情景一:從教室到圖書館,總有少數同學不走人行道而橫穿草坪,這是為什么呢?試用所學數學知識來說明這個問題.

情景二:A、B是河流l兩旁的兩個村莊,現要在河邊修一個抽水站向兩村供水,問抽水站修在什么地方才能使所需的管道最短?請在圖中表示出抽水站點P的位置,并說明你的理由:

你贊同以上哪種做法?你認為應用數學知識為人類服務時應注意什么?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com