【題目】在平面直角坐標系中，菱形OABC的OC邊落在x軸上，∠AOC=60°，OA=60
．若菱形OABC內部（邊界及頂點除外）的一格點P（x，y）滿足：x2﹣y2=90x﹣90y，就稱格點P為“好點”，則菱形OABC內部“好點”的個數為（ ）
（注：所謂“格點”，是指在平面直角坐標系中橫、縱坐標均為整數的點．）
A. 145 B. 146 C. 147 D. 148
【答案】A
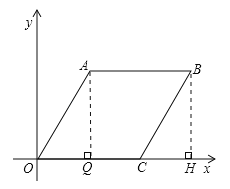
【解析】解：過A作AQ⊥OC于Q，過B作BH⊥X軸于H，∵∠A0C=60°，OA=
，∴∠OAQ=30°，∴OQ=
，由勾股定理得：AQ=90，∵x2﹣y2=90x﹣90y，∴（x﹣y）（x+y﹣90）=0，∴x=y，x+y=90，BH=90 OA：y′=
x
（1）y=x時，令y=90 則x=90，作直線y=x的圖象，交AB于D，∵AQ=90，∴D（90，90）．
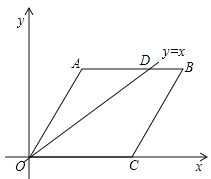
∵邊界及頂點除外
∴y=x時有90﹣1=89個點符合（D點除外），（2）y=﹣x+90時，∵直線OA的解析式為y′=
x，∴令y=y′則x=45（
﹣1）．
∵
≈1.732，∴x≈32.9（取x=33），則直線OA于直線y=﹣x+90的交點是（45
﹣45，135﹣45
），再令y=0 則x=90，∵邊界及頂點除外，∴y=﹣x+90時有90﹣32﹣1=57個點符合，∴有57+89﹣1=145個點符合，故選A．
期末1卷素質教育評估卷系列答案科目：初中數學 來源： 題型：
【題目】如圖，平面直角坐標系中有
三點。
（1）連接
，若
①線段的長為 （直接寫出結果）
②如圖1，點
為
軸負半軸上一點，點
為線段
上一點，連接
作
,且
,當點從
向
運動時，
點不變，
點隨之運動，連接
,求線段的中點
的運動路徑長;
（2）如圖2，作
,連接
并延長，交
延長線于
于
.若
,且
，在平面內是否存在點
,使以
為頂點的四邊形是平行四邊形，若存在，請求出點的坐標;若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖1，已知射線CB∥OA，∠C=∠OAB，
（1）求證：AB∥OC；
（2）如圖2，E、F在CB上，且滿足∠FOB=∠AOB，OE平分∠COF.
①當∠C=110°時，求∠EOB的度數.
②若平行移動AB，那么∠OBC :∠OFC的值是否隨之發生變化？若變化，找出變
化規律；若不變，求出這個比值.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】對于實數a，我們規定：用符號
表示不大于
的最大整數，稱為a的根整數，例如：
，
=3．
(1)仿照以上方法計算：
=______；
=_____．
(2)若
，寫出滿足題意的x的整數值______．
如果我們對a連續求根整數，直到結果為1為止．例如：對10連續求根整數2次
=1，這時候結果為1．
(3)對100連續求根整數，____次之后結果為1．
(4)只需進行3次連續求根整數運算后結果為1的所有正整數中，最大的是____．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】有這樣一個問題：探究函數
的圖象與性質.小華根據學習函數的經驗，對函數的圖象與性質進行了探究.下面是小華的探究過程，請補充完整：
（1）在函數中，自變量x的取值范圍是________．
x | … | -4 | -3 | -2 | -1 | 0 | 1 | 2 | 3 | 4 | … |
y | … | 5 | 4 | 3 | 2 | 1 | 0 | 1 | 2 | m | … |
①求m的值；
②在平面直角坐標系xOy中，描出以上表中各組對應值為坐標的點，并根據描出的點，畫出該函數的圖象．
（2）結合函數圖象寫出該函數的一條性質：________．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，函數y=2x+8的圖象分別交x軸、y軸于A、B兩點，過點A的直線交y軸正半軸于點M，且點M為線段OB的中點．
（1）求直線AM的函數解析式．
（2）試在直線AM上找一點P，使得S△ABP=S△AOB，求出點P的坐標．
（3）若點H為坐標平面內任意一點，在坐標平面內是否存在這樣的點H，使以A、B、M、H為頂點的四邊形是平行四邊形？若存在，請直接寫出所有點H的坐標；若不存在，請說明理由．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】某商場有A、B兩種商品，每件的進價分別為15元、35元.商場銷售5件A商品和2件B商品，可獲得利潤45元;銷售8件A商品和4件B商品，可獲得利潤80元.
(1)求A、B兩種商品的銷售單價;
(2)如果該商場計劃購進A、B兩種商品共80件，用于進貨資金最多投入2 000元，但又要確保獲利至少590元，請問有那幾種進貨方案?
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，反比例函數
的圖象與一次函數y＝mx＋b的圖象交于A（1，3），B（n，－1）兩點.
（1）求反比例函數與一次函數的解析式；
（2）根據圖象回答：當x取何值時，反比例函數的值大于一次函數的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
