
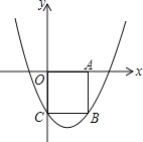
【題目】如圖,在平面直角坐標系xOy中,邊長為2的正方形OABC的頂點A、C分別在x軸正半軸、y軸的負半軸上,二次函數y=![]() (xh)2+k的圖象經過B、C兩點.
(xh)2+k的圖象經過B、C兩點.
(1)求該二次函數的頂點坐標;
(2)結合函數的圖象探索:當y>0時x的取值范圍;
(3)設m<![]() ,且A(m,y1),B(m+1,y2)兩點都在該函數圖象上,試比較y1、y2的大小,并簡要說明理由.
,且A(m,y1),B(m+1,y2)兩點都在該函數圖象上,試比較y1、y2的大小,并簡要說明理由.
【答案】(1)二次函數的頂點坐標為(1,-![]() );(2)x<-1或x>3;(3)y1>y2.
);(2)x<-1或x>3;(3)y1>y2.
【解析】
(1)根據正方形的性質得出點B、C的坐標,根據二次函數的對稱性得出h的數值,再進一步代入一點求出k的數值,即可求出頂點坐標;
(2)由(1)函數解析式求出與x軸交點的坐標解決問題;
(3)根據二次函數的對稱性與點A(m,y1)對稱的點為(2-m,y1),根據圖形,比較得出結論.
解:(1)∵正方形OABC的邊長為2,
∴點B、C的坐標分別為(2,-2),(0,-2),對稱軸x=h=![]() =1,
=1,
把C(0,-2)代入二次函數y=![]() +k,解得k= -
+k,解得k= -![]() ;
;
∴二次函數的頂點坐標為(1,-![]() );
);
(2)當y=0時,![]() =0,解得
=0,解得![]() =-1,
=-1,![]() =3,
=3,
∴當y>0時,x<-1或x>3;
(3)點A(m,y1)關于x=1對稱點為(2-m,y1),
∵m<![]() ,
,
∴m+1<2-m,
∴y1>y2.


科目:初中數學 來源: 題型:
【題目】如圖,已知AD是△ABC的中線,AE=EF=FC,下面給出三個關系式:①AD=2AG;②GE:BE=1:3;③![]() ,其中正確的是( )
,其中正確的是( )

A. ①② B. ①②③ C. ①③ D. ②③
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AD=BC,∠B=∠D,AD不平行于BC,過點C作CE∥AD交△ABC的外接圓O于點E,連接AE.
(1)求證:四邊形AECD為平行四邊形;
(2)連接CO,求證:CO平分∠BCE.

查看答案和解析>>
科目:初中數學 來源: 題型:
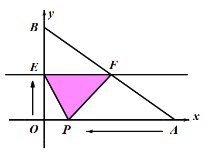
【題目】如圖,已知A,B兩點的坐標分別為(40,0)和(0,30),動點P從點A開始在線段AO上以每秒2個單位長度的速度向原點O運動,同時直線EF由x軸為起始位置以每秒1個單位長度的速度向上平行移動(即EF∥x軸),并且分別與y軸、線段AB交于點E,F,連接EP,FP,設動點P與直線EF同時出發,運動時間為t秒.
(1)求t=15秒時,求EF的長度;
(2)直線EF、點P在運動過程中,是否存在這樣的t,使得△PEF的面積等于160(平方單位)?若存在,請求出此時的值;若不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商貿公司購進某種水果的成本為20元/千克,經過市場調研發現,這種水果在未來48天的售價p(元/千克)與時間t(天)之間的函數表達式為
p=
且其日銷售量y(kg)與時間t(天)的關系如下表:
時間t(天) | 1 | 3 | 6 | 10 | 20 | 40 | … |
日銷售量y(kg) | 118 | 114 | 108 | 100 | 80 | 40 | … |
(1)已知y與t之間的變化規律符合一次函數關系,試求第30天的日銷售量是多少?
(2)問:哪一天的銷售利潤最大?最大日銷售利潤為多少?
(3)在實際銷售的前24天中,公司決定每銷售1 kg水果就捐贈n元利潤(n<9)給“精準扶貧”對象.現發現:在前24天中,每天扣除捐贈后的日銷售利潤隨時間t的增大而增大,求n的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,直線AB與函數y=![]() (x>0)的圖象交于點A(m,2),B(2,n).過點A作AC平行于x軸交y軸于點C,在y軸負半軸上取一點D,使OD=
(x>0)的圖象交于點A(m,2),B(2,n).過點A作AC平行于x軸交y軸于點C,在y軸負半軸上取一點D,使OD=![]() OC,且△ACD的面積是6,連接BC.
OC,且△ACD的面積是6,連接BC.
(1)求m,k,n的值;
(2)求△ABC的面積.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知拋物線![]() 與
與![]() 軸、
軸、![]() 軸分別相交于點A(-1,0)和B(0,3),其頂點為D.
軸分別相交于點A(-1,0)和B(0,3),其頂點為D.
(1)求這條拋物線的解析式;
(2)若拋物線與![]() 軸的另一個交點為E,求△ODE的面積;
軸的另一個交點為E,求△ODE的面積;
(3)拋物線的對稱軸上是否存在點P使得△PAB的周長最短.若存在請求出點P的坐標,若不存在說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(1)問題發現:如圖①,正方形AEFG的兩邊分別在正方形ABCD的邊AB和AD上,連接CF.
①寫出線段CF與DG的數量關系;
②寫出直線CF與DG所夾銳角的度數.
(2)拓展探究:
如圖②,將正方形AEFG繞點A逆時針旋轉,在旋轉的過程中,(1)中的結論是否仍然成立,請利用圖②進行說明.
(2)問題解決
如圖③,△ABC和△ADE都是等腰直角三角形,∠BAC=∠DAE=90°,AB=AC=4,O為AC的中點.若點D在直線BC上運動,連接OE,則在點D的運動過程中,線段OE的長的最小值.(直接寫出結果)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】溫州某企業安排65名工人生產甲、乙兩種產品,每人每天生產2件甲或1件乙,甲產品每件可獲利15元.根據市場需求和生產經驗,乙產品每天產量不少于5件,當每天生產5件時,每件可獲利120元,每增加1件,當天平均每件獲利減少2元.設每天安排x人生產乙產品.
(1)根據信息填表
產品種類 | 每天工人數(人) | 每天產量(件) | 每件產品可獲利潤(元) |
甲 | 15 | ||
乙 |
|
|
(2)若每天生產甲產品可獲得的利潤比生產乙產品可獲得的利潤多550元,求每件乙產品可獲得的利潤.
(3)該企業在不增加工人的情況下,增加生產丙產品,要求每天甲、丙兩種產品的產量相等.已知每人每天可生產1件丙(每人每天只能生產一件產品),丙產品每件可獲利30元,求每天生產三種產品可獲得的總利潤W(元)的最大值及相應的x值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com