【題目】如圖，在
中，
，
平分
，
于點
交于
點，延長
至
使
，連接
．
（1）證明：四邊形
是矩形；
（2）當
時，猜想線段
、
、
的數量關系，并證明．
【答案】（1）詳見解析；（2）
，證明詳見解析
【解析】
(1)根據平行四邊形的性質得到AD∥BC，AD=BC，進而求出AD=FH，再根據平行四邊形的判定得出四邊形AFHD是平形四邊形，最后根據矩形的判定得出即可得到答案；
(2)根據平行四邊形的性質得到AB∥CD，求出∠1=∠3，推出AE=AD，再根據正方形的判定和性質得出AD=DH，求出△DAG≌△DHM，最后根據全等三角形的性質得出∠2=∠3=∠HDM，∠AGD=∠M，求出∠M=∠CDM即可得到答案．
（1）∵四邊形
是平行四邊形
∴
，
（平行四邊形對邊平行且相等），
∵
∴
，
∴
（等量替換），
∴四邊形
是平行四邊形（對邊平行且相等的四邊形是平行四邊形），
∵
∴
，
∴平行四邊形是矩形；
（2）猜想：
證明：如圖，延長
至
使
，連接
，
∵四邊形是平行四邊形，
∴
∴
，
∵
平分
∴
∴
∴
，
∵
∴
，
∴四邊形是正方形，
∴
，
，
在△DAG和△DHM中，
∴
，
∴
，
，
∴
，
∵
，
∴
，
∴
，
∴
，
∵
，，，
∴；
口算題天天練系列答案科目：初中數學 來源： 題型：
【題目】閱讀理（解析）
提出問題：如圖1，在四邊形ABCD中，P是AD邊上任意一點，△PBC與△ABC和△DBC的面積之間有什么關系？探究發現：為了解決這個問題，我們可以先從一些簡單的、特殊的情形入手：
當AP＝
AD時(如圖2)：
∵AP＝AD，△ABP和△ABD的高相等，
∴S△ABP＝S△ABD，
∵PD＝AD﹣AP＝AD，△CDP和△CDA的高相等
∴S△CDP＝S△CDA，
∴S△PBC＝S四邊形ABCD﹣S△ABP﹣S△CDP＝S四邊形ABCD﹣S△ABD﹣S△CDA，
＝S四邊形ABCD﹣(S四邊形ABCD﹣S△DBC)﹣(S四邊形ABCD﹣S△ABC)＝S△DBC+S△ABC.
(1)當AP＝
AD時，探求S△PBC與S△ABC和S△DBC之間的關系式并證明；
(2)當AP＝
AD時，S△PBC與S△ABC和S△DBC之間的關系式為： ；
(3)一般地，當AP＝
AD(n表示正整數)時，探求S△PBC與S△ABC和S△DBC之間的關系為： ；
(4)當AP＝
AD(0≤≤1)時，S△PBC與S△ABC和S△DBC之間的關系式為： ．
查看答案和解析>>
科目：初中數學 來源： 題型：
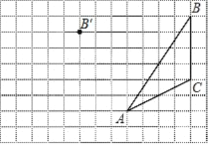
【題目】畫圖并填空：如圖，方格紙中每個小正方形的邊長都為1．在方格紙內將△ABC經過一次平移后得到△A′B′C′，圖中標出了點B的對應點B′．
（1）在給定方格紙中畫出平移后的△A′B′C′；
（2）畫出AB邊上的中線CD
（3）畫出BC邊上的高線AE
（4）點
為方格紙上的格點(異于點
)，若
，則圖中的格點共有 個．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，四邊形ABCD是平行四邊形，P是CD上一點，且AP和BP分別平分∠DAB和∠CBA.
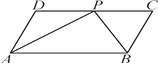
(1)求∠APB的度數；
(2)如果AD＝5 cm，AP＝8 cm，求△APB的周長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中, 
， 
∥
軸， 
.
⑴.求點
的坐標：
⑵.四邊形
的面積
四邊形
；
⑶. 在
軸上是否存在點
,使
△
= 
四邊形
;若存在，求出點
的坐標，若不存在，請說明理由.
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在Rt△ABC中，∠A=90°，AB=AC，BC=20，DE是△ABC的中位線，點M是邊BC上一點，BM=3，點N是線段MC上的一個動點，連接DN，ME，DN與ME相交于點O．若△OMN是直角三角形，則DO的長是______．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在等腰直角三角形ABC中，
D是AB的中點，E，F分別是AC，BC.上的點(點E不與端點A，C重合)，且
連接EF并取EF的中點O，連接DO并延長至點G，使
，連接DE，DF，GE，GF
(1)求證:四邊形EDFG是正方形;
(2)直接寫出當點E在什么位置時，四邊形EDFG的面積最小?最小值是多少?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
