【題目】【探究函數y=x+ 
的圖象與性質】
（1）函數y=x+ 的自變量x的取值范圍是；
（2）下列四個函數圖象中函數y=x+ 的圖象大致是；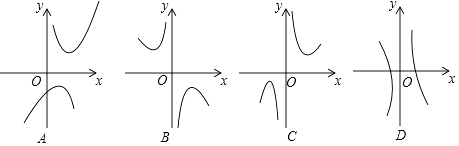 
（3）對于函數y=x+ ，求當x＞0時，y的取值范圍． 請將下列的求解過程補充完整．
解：∵x＞0
∴y=x+ =（ 
）2+（ 
）2=（ ﹣ ）2+
∵（ ﹣ ）2≥0
∴y≥ ．
（4）若函數y= 
，則y的取值范圍 ．
【答案】
（1）x≠0
（2）C
（3）4；4
（4）y≥13
【解析】解：（1）函數y=x+ 
的自變量x的取值范圍是x≠0；（2）函數y=x+ 的圖象大致是C；（3）解：∵x＞0 ∴y=x+ =（ 
）2+（ 
）2=（ ﹣ ）2+4
∵（ ﹣ ）2≥0
∴y≥4．
4）y= 
=x+ 
﹣5═（ ）2+（ 
）2﹣5=（ + ）2+13
∵（ ﹣ ）2≥0，
∴y≥13．
所以答案是：x≠0，C，4，4，y≥13，
【考點精析】解答此題的關鍵在于理解一次函數的性質的相關知識，掌握一般地，一次函數y=kx+b有下列性質：（1）當k>0時，y隨x的增大而增大（2）當k<0時，y隨x的增大而減小，以及對反比例函數的性質的理解，了解性質:當k＞0時雙曲線的兩支分別位于第一、第三象限，在每個象限內y值隨x值的增大而減小； 當k＜0時雙曲線的兩支分別位于第二、第四象限，在每個象限內y值隨x值的增大而增大．
科目：初中數學 來源： 題型：
【題目】如圖，在長方形
中，
cm，
cm，點
為
的中點.若點
在線段
上以1 cm/s的速度由點
向點
運動，到點時不動.同時，點
在線段
上由點向點
運動.
(1)若點的運動速度與點的運動速度相等，經過1 s后，
與
是否全等?請說明理由，并判斷此時線段
和
的位置關系;
(2)若點的運動速度與點的運動速度相等，運動時間為
s，設
的面積為
cm2，請用含的代數式表示
(3)若點的運動速度與點的運動速度不相等，當點的運動速度為多少時，能夠使與全等?
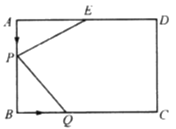
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（3分）如圖，AD是△ABC的角平分線，DE⊥AC，垂足為E，BF∥AC交ED的延長線于點F，若BC恰好平分∠ABF，AE=2BF．給出下列四個結論：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正確的結論共有（ ）
A. 4個 B. 3個 C. 2個 D. 1個
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】（本題9分）把代數式通過配湊等手段，得到完全平方式，再運用完全平方式是非負性這一性質增加問題的條件，這種解題方法叫做配方法．配方法在代數式求值，解方程，最值問題等都有著廣泛的應用．
例如：①用配方法因式分解：a2+6a+8
原式=a2+6a+9－1
=（a+3）2 –1
=（a+3－1）（a+3+1）
=（a+2）（a+4）
②若M=a2－2ab+2b2－2b+2，利用配方法求M的最小值：
a2－2ab+2b2－2b+2=a2－2ab+b2+b2－2b+1+1
=（a－b）2+（b－1）2 +1
∵（a－b）2≥0，（b－1）2 ≥0
∴當a=b=1時，M有最小值1
請根據上述材料解決下列問題：
（1）在橫線上添上一個常數項使之成為完全平方式：a 2+4a+ ．
（2）用配方法因式分解： a2－24a+143
（3）若M=
a2+2a +1，求M的最小值．
（4）已知a2+b2+c2－ab－3b－4c+7=0，求a+b+c的值．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平行四邊形ABCD中，按以下步驟作圖：①以A為圓心，任意長為半徑作弧，分別交AB，AD于點M，N；②分別以M，N為圓心，以大于 
MN的長為半徑作弧，兩弧相交于點P；③作AP射線，交邊CD于點Q，若DQ=2QC，BC=3，則平行四邊形ABCD周長為 ．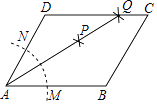 
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在△ABC和△DBE中，BC=BE，還需要添加兩個條件才能使△ABC≌△DBE，則不能添加的一組條件是（ ）
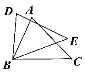
A. AC=DE，∠C=∠E B. BD=AB，AC=DE C. AB=DB，∠A=∠D D. ∠C=∠E，∠A=∠D
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
