
【題目】霧霾天氣已經成為人們普遍關注的話題,霧霾不僅僅影響人們的出行,還影響著人們的健康,太原市會持續出現霧霾天氣嗎?在2016年2月周末休息期間,某校九年級1班綜合實踐小組的同學以“霧霾天氣的主要成因”為主題,隨機調查了太原市部分市民的觀點,并對調查結果進行了整理,繪制了如下不完整的統計圖表,觀察并回答下列問題:
類別 | 霧霾天氣的主要成因 | 百分比 |
A | 工業污染 | 45% |
B | 汽車尾氣排放 | m |
C | 城中村燃煤問題 | 15% |
D | 其他(綠化不足等) | n |
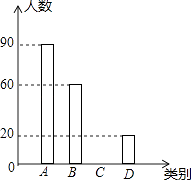
(1)請你求出本次被調查市民的人數及m,n的值,并補全條形統計圖;
(2)若太原市有300萬人口,請你估計持有A,B兩類看法的市民共有多少人?
(3)學校要求小穎同學在A,B,C,D這四個霧霾天氣的主要成因中,隨機抽取兩項作為課題研究的項目進行考察分析,請用畫樹狀圖或列表的方法,求出小穎同學剛好抽到B(汽車尾氣排放),C(城中村燃煤問題)的概率.(用A,B,C,D表示各項目)
【答案】
(1)解:本次被調查的市民共有:90÷45%=200(人),
B類所占的百分比是:m= ![]() ×100%=30%;
×100%=30%;
D類所占的百分比是:n=1﹣45%﹣30%=10%=10%;
C類的人數是:200×15%=30(人),
補圖如下:
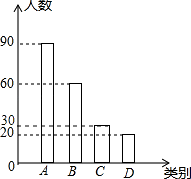
(2)解:根據題意得:300×(45%+30%)=225(萬人).
答:持有A、B兩類看法的市民共有人數為75萬人
(3)解:畫樹狀圖得:
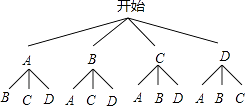
∵共有12種等可能的結果,小穎同學剛好抽到B(汽車尾氣排放),C(城中村燃煤問題)的有2種情況,
∴小穎同學剛好抽到B(汽車尾氣排放),C(城中村燃煤問題)的概率為: ![]() =
= ![]()
【解析】(1)用A類的人數除以所占的百分比求出被調查的市民數,再用B類的人數除以總人數得出B類所占的百分比,再用總人數乘以C類所占的百分比求出C類的人數,從而補全統計圖;(2)用該市的總人數乘以持有A、B兩類的所占的百分比即可;(3)首先根據題意畫出樹狀圖,然后由樹狀圖求得所有等可能的結果與小穎同學剛好抽到B(汽車尾氣排放),C(城中村燃煤問題)的情況,再利用概率公式即可求得答案.
【考點精析】關于本題考查的統計表和條形統計圖,需要了解制作統計表的步驟:(1)收集整理數據.(2)確定統計表的格式和欄目數量,根據紙張大小制成表格.(3)填寫欄目、各項目名稱及數據.(4)計算總計和合計并填入表中,一般總計放在橫欄最左格,合計放在豎欄最上格.(5)寫好表格名稱并標明制表時間;能清楚地表示出每個項目的具體數目,但是不能清楚地表示出各個部分在總體中所占的百分比以及事物的變化情況才能得出正確答案.


 快樂小博士鞏固與提高系列答案
快樂小博士鞏固與提高系列答案科目:初中數學 來源: 題型:
【題目】問題背景
在數學活動課上,張老師要求同學們拿兩張大小不同的矩形紙片進行旋轉變換探究活動.如圖1,在矩形紙片ABCD和矩形紙片EFGH中,AB=1,AD=2,且EF>AD,FG>AB,點E是AD的中點,矩形紙片EFGH以點E為旋轉中心進行逆時針旋轉,在旋轉過程中會產生怎樣的數量關系,提出恰當的數學問題并加以解決.
解決問題
下面是三個學習小組提出的數學問題,請你解決這些問題.
(1)“奮進”小組提出的問題是:如圖1,當EF與AB相交于點M,EH與BC相交于點N時,求證:EM=EN.
(2)“雄鷹”小組提出的問題是:在(1)的條件下,當AM=CN時,AM與BM有怎樣的數量關系,說明理由.
(3)“創新”小組提出的問題是;若矩形EFGH繼續以點E為旋轉中心進行逆時針旋轉,當∠AEF=60°時,請你在圖2中畫出旋轉后的示意圖,并求出此時EF將邊BC分成的兩條線段的長度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖(1)所示,∠AOB、∠COD都是直角.
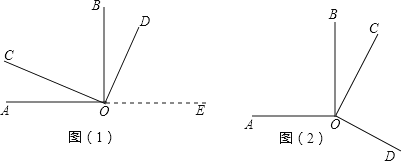
(1)試猜想∠AOD與∠COB在數量上是相等,互余,還是互補的關系.請你用推理的方法說明你的猜想是合理的.
(2)當∠COD繞著點O旋轉到圖(2)所示位置時,你在(1)中的猜想還成立嗎?請你證明你的結論.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在正方形網格中,我們把,每個小正方形的頂點叫做格點,連接任意兩個格點的線段叫網格線段,以網格線段為邊組成的圖形叫做格點圖形,在下列如圖所示的正方形網格中,每個小正方形的邊長為1. 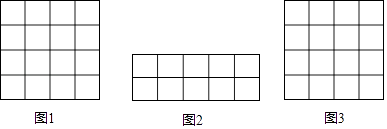
(1)請你在圖1中畫一個格點圖形,且該圖形是邊長為 ![]() 的菱形;
的菱形;
(2)請你在圖2中用網格線段將其切割成若干個三角形和正方形,拼接成一個與其面積相等的正方形,并在圖3中畫出格點正方形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A是拋物線y= ![]() x2上的一個動點,且點A在第一象限內.AE⊥y軸于點E,點B坐標為(0,2),直線AB交x軸于點C,點D與點C關于y軸對稱,直線DE與AB相交于點F,連結BD.設線段AE的長為m,△BED的面積為S.
x2上的一個動點,且點A在第一象限內.AE⊥y軸于點E,點B坐標為(0,2),直線AB交x軸于點C,點D與點C關于y軸對稱,直線DE與AB相交于點F,連結BD.設線段AE的長為m,△BED的面積為S.
(1)當m= ![]() 時,求S的值.
時,求S的值.
(2)求S關于m(m≠2)的函數解析式.
(3)①若S= ![]() 時,求
時,求 ![]() 的值;
的值;
②當m>2時,設 ![]() =k,猜想k與m的數量關系并證明.
=k,猜想k與m的數量關系并證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】定義:如果10b=n,那么稱b為n的勞格數,記為b= d(n).
(1)根據勞格數的定義,可知d(10)=1,d(102)=2,直接寫出 d(103)的值.
(2)勞格數有如下運算性質:若m,n為正數,則d(mn)= d(m)+ d(n);d(![]() )= d(m)- d(n).
)= d(m)- d(n).
根據運算性質,求:![]() ,若
,若 ![]() ,直接寫出
,直接寫出![]() ,
,![]() 的值.
的值.
(3)下表中與數x對應的勞格數 ![]() 有且只有兩個是錯誤的,請找出錯誤的勞格數并改正.
有且只有兩個是錯誤的,請找出錯誤的勞格數并改正.
| 1.5 | 3 | 5 | 6 | 8 | 9 | 12 | 27 |
|
|
|
|
|
|
|
|
|
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知直線PD垂直平分⊙O的半徑OA于點B,PD交⊙O于點C、D,PE是⊙O的切線,E為切點,連結AE,交CD于點F. 
(1)若⊙O的半徑為8,求CD的長;
(2)證明:PE=PF;
(3)若PF=13,sinA= ![]() ,求EF的長.
,求EF的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com