
【題目】如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.動點M,N從點C同時出發,均以每秒1cm的速度分別沿CA、CB向終點A,B移動,同時動點P從點B出發,以每秒2cm的速度沿BA向終點A移動,連接PM,PN,設移動時間為t(單位:秒,0<t<2.5).
(1)當t為何值時,以A,P,M為頂點的三角形與△ABC相似?
(2)是否存在某一時刻t,使四邊形APNC的面積S有最小值?若存在,求S的最小值;若不存在,請說明理由.
【答案】
(1)解:∵如圖,在Rt△ABC中,∠C=90°,AC=4cm,BC=3cm.
∴根據勾股定理,得AB= ![]() 。(1)以A,P,M為頂點的三角形與△ABC相似,分兩種情況:①當△AMP∽△ABC時,
。(1)以A,P,M為頂點的三角形與△ABC相似,分兩種情況:①當△AMP∽△ABC時, ![]() ,即
,即 ![]() ,解得
,解得 ![]() ; ②當△APM∽△ABC時,
; ②當△APM∽△ABC時, ![]() ,即
,即 ![]() ,解得t=0(不合題意,舍去)。
,解得t=0(不合題意,舍去)。
綜上所述,當 ![]() 時,以A、P、M為頂點的三角形與△ABC相似
時,以A、P、M為頂點的三角形與△ABC相似
(2)解:存在某一時刻t,使四邊形APNC的面積S有最小值.
理由如下:假設存在某一時刻t,使四邊形APNC的面積S有最小值。如圖,過點P作PH⊥BC于點H.則PH∥AC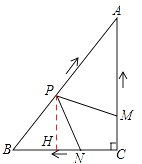
∴ ![]() ,即
,即 ![]() 。
。
∴ ![]() ∴
∴ ![]()
∵ ![]() >0,
>0,
∴S有最小值。當t= ![]() 時,S最小值=
時,S最小值= ![]() . 答:當t=
. 答:當t= ![]() 時,四邊形APNC的面積S有最小值,其最小值是
時,四邊形APNC的面積S有最小值,其最小值是 ![]()
【解析】(1)根據△AMP∽△ABC,可得成比例的線段,問題得解;(2)首先假設存在某一時刻t,使四邊形APNC的面積S有最小值,然后把四邊形APNC的面積表示出來,其面積是一個二次函數,再根據二次函數的性質求解。
【考點精析】利用二次函數的最值和相似三角形的判定與性質對題目進行判斷即可得到答案,需要熟知如果自變量的取值范圍是全體實數,那么函數在頂點處取得最大值(或最小值),即當x=-b/2a時,y最值=(4ac-b2)/4a;相似三角形的一切對應線段(對應高、對應中線、對應角平分線、外接圓半徑、內切圓半徑等)的比等于相似比;相似三角形周長的比等于相似比;相似三角形面積的比等于相似比的平方.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB∥CD,∠BAD、∠ADC的平分線AE、DF分別與線段BC相交于點E、F,∠DFC=30°,AE與DF相交干點G,則∠AEC=________.

查看答案和解析>>
科目:初中數學 來源: 題型:
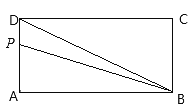
【題目】如圖,長方形ABCD中,AB=2cm,BC=4cm,點P按照順時針方向由點A運動到點D,設點P運動的路程為![]() 圖中點P、B、D圍成的圖形的面積為
圖中點P、B、D圍成的圖形的面積為![]()
(1)寫出點P、B、D圍成的圖形的面積![]() 與
與![]() 之間的關系式和自變量
之間的關系式和自變量![]() 的取值范圍;
的取值范圍;
(2)當![]() 取何值時,點P、B、D圍成的圖形的面積等于
取何值時,點P、B、D圍成的圖形的面積等于![]() ?
?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題,正確的有( )
①經過三個點一定可以作圓;②任意一個三角形一定有一個外接圓,并且只有一個外接圓;③在同圓或等圓中,相等的弦則所對的弧相等;④正多邊形既是中心對稱圖形又是軸對稱圖形;⑤三角形的內心到三角形各邊的距離相等.
A.![]() 個B.
個B.![]() 個C.
個C.![]() 個D.
個D.![]() 個
個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系中,A,B,C三點的坐標分別為(-6,7)、(-3,0)、(0,3).

(1)畫出△ABC,并求△ABC的面積.
(2)在平面直角坐標系中平移△ABC,使點C經過平移后的對應點為C'(5,4),平移后△ABC得到△A'B'C',畫出平移后的△A'B'C',并寫出點A',B'的坐標
(3)P(-3,m)為△ABC中一點,將點P向右平移4個單位后,再向上平移6個單位得到點Q(n,-3),則m= n=
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,D是AB的中點,E是CD的中點,過點C作CF∥AB交AE的延長線于點F,連結BF.

(1)求證:四邊形BDCF是平行四邊形;
(2)當AC=BC時,判斷四邊形BDCF是哪種特殊的平行四邊形,并證明你的結論.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com