Question

【題目】如圖①，在等邊三角形ABC中．D是AB邊上的動點，以CD為一邊，向上作等邊三角形EDC．連接AE.

(l)求證：△DBC≌△EAC

(2)試說明AE∥BC的理由．

(3)如圖②，當圖①中動點D運動到邊BA的延長線上時，所作仍為等邊三角形，猜想是否仍有AE∥BC?若成立請證明．

Answer 1

【答案】（1）見解析；（2）見解析；（3）仍有AE∥BC，理由見解析

【解析】試題分析：（1）根據△ABC與△EDC是等邊三角形，利用其三邊相等和三角相等的關系，求證∠BCD=∠ACE．然后即可證明結論；

（2）根據ACE≌△BCD，可得∠ABC=∠CAE=60°，利用等量代換求證∠CAE=∠ACB即可．

（3）證明△DBC≌△EAC可推出∠EAC=∠ACB，由此可證．

試題解析：（1）∵∠ACB=60， ∠DCE=60，

∴∠BCD=60-∠ACD， ∠ACE=60-∠ACD，

即∠BCD=∠ACE，

在△DBC和△EAC中，

，

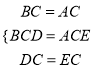∴△DBC≌△EAC(SAS)；

（2） ∵△DBC≌△EAC，

∴∠EAC=∠B=60，

又∵∠ACB=60，

∴∠EAC=∠ACB，

∴AE∥BC；

（3）仍有AE∥BC，

∵△ABC，△EDC都為等邊三角形，

∴BC=AC， DC=CE， ∠BCA=∠DCE=60，

∴∠BCA+∠ACD=∠DCE+∠ACD，

即∠BCD=∠ACE，

在△DBC和△EAC中，

，

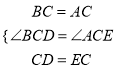∴△DBC和△EAC(SAS)，

∴∠EAC=∠B=60，

又∵∠ACB=60，

∴∠EAC=∠ACB，

∴AE∥BC.