
【題目】如圖,在△ABC中,AB=AC,∠BAC=50°,∠BAC的平分線與AB的垂直平分線交于點O,將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,則∠CFE為________度.

【答案】50°
【解析】
連接OB,OC,先求出∠BAO=25°,進而求出∠OBC=40°,求出∠COE=∠OCB=40°,最后根據等腰三角形的性質,問題即可解決.
解:如圖,連接OB,
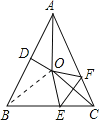
∵∠BAC=50°,AO為∠BAC的平分線,
∴∠BAO=![]() ∠BAC=
∠BAC=![]() ×50°=25°.
×50°=25°.
又∵AB=AC,
∴∠ABC=∠ACB=65°.
∵DO是AB的垂直平分線,
∴OA=OB,
∴∠ABO=∠BAO=25°,
∴∠OBC=∠ABC-∠ABO=65°-25°=40°.
∵AO為∠BAC的平分線,AB=AC,
∴直線AO垂直平分BC,
∴OB=OC,
∴∠OCB=∠OBC=40°,
∵將∠C沿EF(E在BC上,F在AC上)折疊,點C與點O恰好重合,
∴OE=CE.
∴∠COE=∠OCB=40°;
在△OCE中,∠OEC=180°-∠COE-∠OCB=180°-40°-40°=100°,
∴∠CEF=![]() ∠CEO=50°.
∠CEO=50°.
故答案為:50°.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數學 來源: 題型:
【題目】某科技有限公司準備購進A和B兩種機器人來搬運化工材料,已知購進A種機器人2個和B種機器人3個共需16萬元;購進A種機器人3個和B種機器人2個共需14萬元.請解答下列問題:
(1)求A , B兩種機器人每個的進價;
(2)已知該公司購買B種機器人的個數比購買A種機器人的個數的2倍多4個,如果需要購買A、B兩種種機器人的總個數不少于28個,且該公司購買的A、B兩種種機器人的總費用不超過106萬元,那么該公司有哪幾種購買方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知,BC∥OA,∠B=∠A=100°,試回答下列問題:

(1)如圖①,求證:OB∥AC.
(2)如圖②,若點E、F在線段BC上,且滿足∠FOC=∠AOC,并且OE平分∠BOF.求∠EOC的度數.
(3)在(2)的條件下,若平行移動AC,如圖③,那么∠OCB:∠OFB的值是否隨之發生變化?若變化,試說明理由;若不變,求出這個比值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知,AD是△ABC的內角平線,交BC于D點,DE⊥AB,DF⊥AC,垂足分別為E、F,連結EF,
(1)請根據上述幾何語言,畫出完整的圖形,作∠BAC的角平分線AD要求尺規作圖,(保留作圖痕跡,不寫作法);
(2)判斷AD是否為EF的垂直平分線,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,是拋物線y=ax2+bx+c(a≠0)圖象的一部分,已知拋物線的對稱軸為x=2,與x軸的一個交點是(﹣1,0).下列結論:
①ac<0;
②4a﹣2b+c>0;
③拋物線與x軸的另一個交點是(4,0);
④點(﹣3,y1),(6,y2)都在拋物線上,則有y1<y2 . 其中正確的個數為( )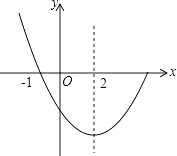
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在 ![]() ABC中,AD平分
ABC中,AD平分 ![]() BAC,按如下步驟作圖:
BAC,按如下步驟作圖:
第一步,分別以點A、D為圓心,以大于 ![]() AD的長為半徑在AD兩側做弧,交于兩點M、N;
AD的長為半徑在AD兩側做弧,交于兩點M、N;
第二步,連接MN分別交AB、AC于點E、F;
第三步,連接DE、DF.
若BD=6,AF=4,CD=3,則BE的長是( ).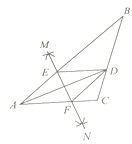
A.2
B.4
C.6
D.8
查看答案和解析>>
科目:初中數學 來源: 題型:
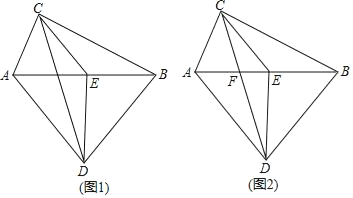
【題目】如圖,已知AC⊥BC,AD⊥BD,E為AB的中點,
(1)如圖1,求證:△ECD是等腰三角形;
(2)如圖2,CD與AB交點為F,若AD=BD,EF=3,DE=4,求CD的長.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com