
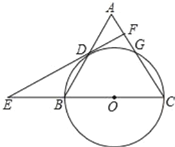
【題目】如圖,在![]() ABC中,CA=CB=10,AB=12,以BC為直徑的圓⊙O交AC于點G,交AB于點D,過點D作⊙O的切線,交CB的延長線于點E,交AC于點F.則下列結(jié)論正確的是_____
ABC中,CA=CB=10,AB=12,以BC為直徑的圓⊙O交AC于點G,交AB于點D,過點D作⊙O的切線,交CB的延長線于點E,交AC于點F.則下列結(jié)論正確的是_____
①DF⊥AC; ②DO=DB; ③S△ABC=48; ④cos∠E=![]() .
.
【答案】①③④
【解析】
連接OD,BG,CD,如圖,利用切線的性質(zhì)得到OD⊥DF,再利用圓周角定理和等腰三角形的性質(zhì)證明OD∥AC,則可對①進行判斷;利用OB=![]() BC=5,BD=6可對②進行判斷;利用勾股定理計算出CD=8,則可計算出
BC=5,BD=6可對②進行判斷;利用勾股定理計算出CD=8,則可計算出![]() ABC的面積,從而可對③進行判斷;利用面積法計算出BG=
ABC的面積,從而可對③進行判斷;利用面積法計算出BG=![]() ,則cos∠CBG=
,則cos∠CBG=![]() ,然后證明∠E=∠CBG,從而可對④進行判斷.
,然后證明∠E=∠CBG,從而可對④進行判斷.
解:連接OD,BG,CD,如圖,
∵DF為切線,
∴OD⊥DF,
∵BC為直徑,
∴∠BDC=90°,
∵CA=CB,
∴CD平分AB,即AD=BD=6,
而OB=OC,
∴OD為![]() ABC的中位線,
ABC的中位線,
∴OD∥AC,
∴DF⊥AC,所以①正確;
∵OB=![]() BC=5,BD=6,
BC=5,BD=6,
∴OD≠BD,所以②錯誤;
在Rt![]() BCD中,CD=
BCD中,CD=![]() =8,
=8,
∴S△ABC=![]() CDAB=
CDAB=![]() ×8×12=48,所以③正確;
×8×12=48,所以③正確;
∵BC為直徑,
∴∠BGC=90°,
∴S△ABC=![]() BGAC=48,
BGAC=48,
∴BG=![]() ,
,
∴cos∠CBG=![]() =
=![]() =
=![]() ,
,
∵BG⊥AC,EF⊥AC,
∴BG∥EF,
∴∠E=∠CBG,
∴cos∠E=![]() ,所以④正確.
,所以④正確.
故答案為:①③④.



科目:初中數(shù)學(xué) 來源: 題型:
【題目】自行車因其便捷環(huán)保深受人們喜愛,成為日常短途代步與健身運動首選.如圖1是某品牌自行車的實物圖,圖2是它的簡化示意圖.經(jīng)測量,車輪的直徑為![]() ,中軸軸心
,中軸軸心![]() 到地面的距離
到地面的距離![]() 為
為![]() ,后輪中心
,后輪中心![]() 與中軸軸心
與中軸軸心![]() 連線與車架中立管
連線與車架中立管![]() 所成夾角
所成夾角![]() ,后輪切地面
,后輪切地面![]() 于點
于點![]() .為了使得車座
.為了使得車座![]() 到地面的距離
到地面的距離![]() 為
為![]() ,應(yīng)當(dāng)將車架中立管
,應(yīng)當(dāng)將車架中立管![]() 的長設(shè)置為_____________
的長設(shè)置為_____________![]() .
.
(參考數(shù)據(jù): ![]()
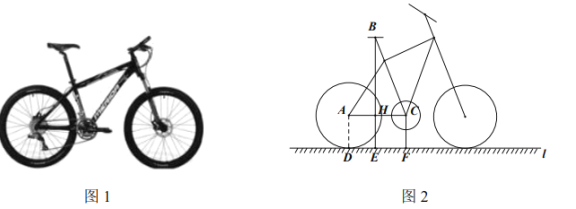
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖1,已知![]() 中,
中,![]() ,
,![]() ,點
,點![]() 在
在![]() 邊的延長線上,且
邊的延長線上,且![]() .
.
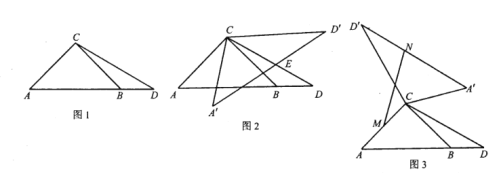
(1)求![]() 的度數(shù);
的度數(shù);
(2)如圖2,將![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() (
(![]() )得到
)得到![]() .
.
①若![]() ,
,![]() 與
與![]() 相交于點
相交于點![]() ,求
,求![]() 的長度;
的長度;
②連接![]() ,
,![]() ,若旋轉(zhuǎn)過程中
,若旋轉(zhuǎn)過程中![]() 時,求滿足條件的
時,求滿足條件的![]() 的度數(shù).
的度數(shù).
(3)如圖3,將![]() 繞點
繞點![]() 逆時針旋轉(zhuǎn)
逆時針旋轉(zhuǎn)![]() (
(![]() )得到
)得到![]() ,若點
,若點![]() 為
為![]() 的中點,點
的中點,點![]() 為線段
為線段![]() 上任意一點,直接寫出旋轉(zhuǎn)過程中,線段
上任意一點,直接寫出旋轉(zhuǎn)過程中,線段![]() 長度的取值范圍為______.
長度的取值范圍為______.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】已知關(guān)于x的一元二次方程x2﹣(m+2)x+2m=0.
(1)求證:不論m為何值,該方程總有兩個實數(shù)根;
(2)若直角△ABC的兩直角邊AB、AC的長是該方程的兩個實數(shù)根,斜邊BC的長為3,求m的值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
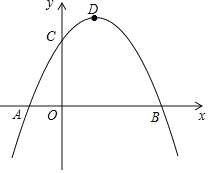
【題目】如圖,已知拋物線交x軸于A、B兩點,交y軸于C點,A點坐標(biāo)為(﹣1,0),OC=2,OB=3,點D為拋物線的頂點.
(1)求拋物線的解析式;
(2)P為坐標(biāo)平面內(nèi)一點,以B、C、D、P為頂點的四邊形是平行四邊形,求P點坐標(biāo);
(3)若拋物線上有且僅有三個點M1、M2、M3使得△M1BC、△M2BC、△M3BC的面積均為定值S,求出定值S及M1、M2、M3這三個點的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某校興趣小組以問卷調(diào)查的形式,隨機調(diào)查了某地居民對武漢封城后續(xù)措施的了解情況,設(shè)置了多選題,并將調(diào)查結(jié)果繪制成如圖不完整的統(tǒng)計圖.
選項 | A | B | C | D | E |
后續(xù)措施 | 擴大宣傳力度 | 分類隔離病人 | 封閉小區(qū) | 聘請專業(yè)物資 | 采取其他措施 |
選擇人次 | 25 | 85 | 15 | 35 |

已知平均每人恰好選擇了兩個選項,根據(jù)以上信息回答下列問題:
(1)求參與本次問卷調(diào)查的居民人數(shù),并補全條形統(tǒng)計圖;
(2)在扇形統(tǒng)計圖中,求E選項對應(yīng)圓心角α的度數(shù);
(3)根據(jù)此次調(diào)查結(jié)果估計該地100萬居民當(dāng)中選擇D選項的人數(shù).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
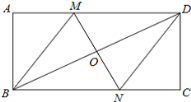
【題目】如圖,在矩形ABCD中,對角線BD的垂直平分線MN與AD相交于點M,與BC相交于點N.連接BM,DN.
(1)求證:四邊形BMDN是菱形;
(2)若AB=4,AD=8,求MD的長.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】在平面直角坐標(biāo)系中,點![]() 在拋物線上,將拋物線
在拋物線上,將拋物線![]() 在點
在點![]() 右側(cè)的部分沿著直線
右側(cè)的部分沿著直線![]() 翻折,翻折后的圖象與原拋物線剩余部分合稱為圖象
翻折,翻折后的圖象與原拋物線剩余部分合稱為圖象![]() .
.
(1)當(dāng)![]() 時,
時,
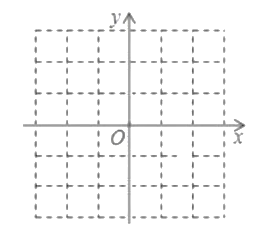
①在如圖的平面直角坐標(biāo)系中畫出圖象![]() ;
;
②直接寫出圖象![]() 對應(yīng)函數(shù)的表達式;
對應(yīng)函數(shù)的表達式;
③當(dāng)![]() 時,圖象
時,圖象![]() 對應(yīng)函數(shù)的最小值為
對應(yīng)函數(shù)的最小值為![]() 求
求![]() 的取值范圍.
的取值范圍.
(2)當(dāng)![]() 時,直接寫出圖象
時,直接寫出圖象![]() 對應(yīng)函數(shù)
對應(yīng)函數(shù)![]() 隨
隨![]() 增大而減小時
增大而減小時![]() 的取值范圍.
的取值范圍.
(3)若圖象![]() 上有且只有三個點到直線
上有且只有三個點到直線![]() 的距離為
的距離為![]() ,直接寫出
,直接寫出![]() 的值.
的值.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com