
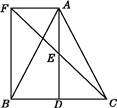
【題目】如圖,△ABC中,D是BC邊上的一點,E為AD的中點,過A作BC的平行線交CE的延長線于F,且AF=BD,連接BF.
(1)求證:BD=CD;
(2)如果AB=AC,試判斷四邊形AFBD的形狀,并證明你的結論.
【答案】(1)證明見解析;(2)當AB=AC時,四邊形AFBD是矩形,證明見解析.
【解析】試題分析:(1)根據平行線的性質得到∠AFE=∠DCE,由中點的定義得到AE=DE,根據三角形全等的判定易證得△AFE≌△DCE,利用全等三角形的性質得AF=DC,而AF=BD,即可得到D是BC的中點;
(2)在(1)的基礎上,根據全等三角形的性質和有三個角都是直角的四邊形是矩形.
試題解析:證明:∵AF∥BC,∴∠AFE=∠ECD.
又∵E為AD的中點,∴AE=DE.
在△AFE與△DCE中,∵ 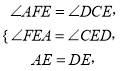
∴△AFE≌△DCE(AAS),∴AF=CD.
又∵AF=BD,∴BD=CD.
(2)解:當AB=AC時,四邊形AFBD是矩形.
證法一:由(1)知,D為BC的中點,又∵AB=AC,
∴AD⊥BC.
∵AF∥BC,∴∠DAF=∠ADB=90°.
∵△AFE≌△DCE(已證),∴CE=EF.
∴DE為△BCF的中位線,∴DE∥BF.
∴∠FBD=∠EDC=90°,
∴四邊形AFBD是矩形.
證法二:∵AF=BD,AF∥BD,
∴四邊形AFBD是平行四邊形.
由(1)知,D為BC的中點,又∵AB=AC,
∴AD⊥BC(三線合一),即∠BDA=90°.
∴AFBD是矩形.


 口算題天天練系列答案
口算題天天練系列答案科目:初中數學 來源: 題型:
【題目】如圖所示,小明家小區空地上有兩棵筆直的樹![]() 、
、![]() .一天,他在
.一天,他在![]() 處測得樹頂
處測得樹頂![]() 的仰角
的仰角![]() ,在
,在![]() 處測得樹頂
處測得樹頂![]() 的仰角
的仰角![]() ,線段
,線段![]() 恰好經過樹頂
恰好經過樹頂![]() .已知.
.已知. ![]() 、
、![]() 兩處的距離為
兩處的距離為![]() 米,兩棵樹之間的距離
米,兩棵樹之間的距離![]() 米,
米, ![]() 、
、![]() 、
、![]() 、
、![]() 四點在一條直線上,求樹
四點在一條直線上,求樹![]() 的高度.(
的高度.(![]() ,
, ![]() ,結果精確到
,結果精確到![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各組數中,以a、b、c為邊的三角形不是直角三角形的是( )
A. a=![]() ,b=
,b=![]() ,c=
,c=![]() B. a=1.5,b=2,c=3
B. a=1.5,b=2,c=3
C. a=6,b=8,c=10 D. a=3,b=4,c=5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商品的進價為每件50元,售價為每件60元,每天可賣出190件;如果每件商品的售價每上漲1元,則每天少賣10件,設每件商品的售價上漲x元,每天的銷售利潤為y元.
(1)求y關于x的關系式;
(2)每件商品的售價定為多少元時,每天的利潤恰為1980元?
(3)每件商品的售價定為多少元時,每天可獲得最大利潤?最大利潤是多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知關于x,y的方程組![]() 的解滿足x<0,y>0.
的解滿足x<0,y>0.
(1)x=________, y=________(用含a的代數式表示);
(2)求a的取值范圍;
(3)若2x8y=2m,用含有a的代數式表示m,并求m的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】古代絲綢之路上的花剌子模地區曾經誕生過一位偉大的數學家-“代數學之父”阿爾·花拉子米.在研究一元二次方程解法的過程中,他覺得“有必要用幾何學方式來證明曾用數字解釋過的問題的正確性”.

以![]() 為例,花拉子米的幾何解法如下:
為例,花拉子米的幾何解法如下:
如圖,在邊長為![]() 的正方形的兩個相鄰邊上作邊長分別為
的正方形的兩個相鄰邊上作邊長分別為![]() 和5的矩形,再補上一個邊長為5的小正方形,最終把圖形補成一個大正方形.
和5的矩形,再補上一個邊長為5的小正方形,最終把圖形補成一個大正方形.
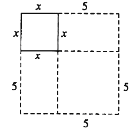
通過不同的方式來表達大正方形的面積,可以將原方程化為![]() )2=39+ ,從而得到此方程的正根是 .
)2=39+ ,從而得到此方程的正根是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題:①相等的角是對頂角;②在同一平面內,若a∥b,b∥c,則a∥c;③同旁內角互補;④互為鄰補角的兩角的角平分線互相垂直.⑤平面內,過一點能且只能作一條直線與已知直線垂直.其中真命題有______(填序號)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某劇院觀眾席的座位設置為扇形,且按下列方式排布:

(1)按照上表所表示的變化規律,當排數![]() 每增加1時,座位數
每增加1時,座位數![]() 如何變化?
如何變化?
(2)寫出座位數![]() 與排數
與排數![]() 之間的關系式.
之間的關系式.
(3)按照上表所示的規律,某一排可能有90個座位嗎?說說你的理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com