
【題目】如圖,在等邊三角形ABC中,AE=CD,AD、BE交于Q點,BP⊥AD于P點. 
求證:
(1)△BAE≌△ACD;
(2)∠BQP=60°;
(3)BQ=2PQ.
【答案】
(1)證明:∵△ABC是等邊三角形,
∴AB=AC,∠BAE=∠C=60°,
在△ABE和△CAD中,
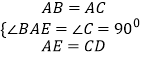 ,
,
∴△ABE≌△CAD(SAS)
(2)∵△ABE≌△CAD
∴∠1=∠2,
∴∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°
(3)∵BQ⊥AD,
∴∠PBQ=90°﹣∠BPQ=90°﹣60°=30°,
∴BP=2PQ.
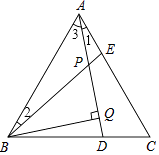
【解析】(1)由AB=AC,∠BAE=∠C,AE=CD,即可證明.(2)根據三角形的外角的性質,∠BPQ=∠2+∠3=∠1+∠3=∠BAC=60°,即可證明.(3)利用直角三角形30度性質即可解決問題.
【考點精析】利用等邊三角形的性質對題目進行判斷即可得到答案,需要熟知等邊三角形的三個角都相等并且每個角都是60°.


科目:初中數學 來源: 題型:
【題目】下列說法正確的是( )
A.擲一枚硬幣,正面一定朝上
B.某種彩票中獎概率為1%,是指買100張彩票一定有1張中獎
C.旅客上飛機前的安檢應采用抽樣調查
D.方差越大,數據的波動越大
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,半圓O的直徑AB=4,以長為2的弦PQ為直徑,向點O方向作半圓M,其中P點在弧AQ上且不與A點重合,但Q點可與B點重合.
(1)弧AP的長與弧QB的長之和為定值l,請直接寫出l的值;
(2)請直接寫出點M與AB的最大距離,此時點P,A間的距離;點M與AB的最小距離,此時半圓M的弧與AB所圍成的封閉圖形面積.
(3)當半圓M與AB相切時,求弧AP的長.
(注:結果保留π,cos 35°=![]() ,cos 55°=
,cos 55°=![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為了節約用水,某市決定調整居民用水收費方法,規定:
①如果每戶每月水不超過![]() 噸,每噸水收費
噸,每噸水收費![]() 元.
元.
②如果每戶每月用水超過![]() 噸,則超過部分每噸水收費
噸,則超過部分每噸水收費![]() 元.
元.
小紅看到這種收費方法后,想算算她家每月的水費,但是她不清楚家里每月的用水是否超過![]() 噸.
噸.
(![]() )如果小紅家每月用水
)如果小紅家每月用水![]() 噸,水費是多少?如果每月用水
噸,水費是多少?如果每月用水![]() 噸,水費是多少?
噸,水費是多少?
(![]() )如果字母
)如果字母![]() 表示小紅家每月用水的噸數,那么小紅家每月的水費該如何用
表示小紅家每月用水的噸數,那么小紅家每月的水費該如何用![]() 的代數式表示呢?
的代數式表示呢?
查看答案和解析>>
科目:初中數學 來源: 題型:
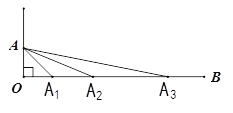
【題目】如圖,已知![]() ,點
,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上,點
上,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上,點
上,點![]() 繞點
繞點![]() 順時針旋轉后的對應點
順時針旋轉后的對應點![]() 落在射線
落在射線![]() 上,…,連接
上,…,連接![]() 、
、![]() 、
、![]() …,以此作法,則
…,以此作法,則![]() =______度.(用含
=______度.(用含![]() 的代數式表示,
的代數式表示, ![]() 為正整數)
為正整數)
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com