
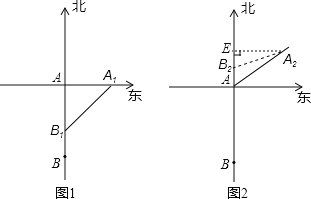
【題目】如圖,一艘輪船以30海里/小時的速度由西向東航行,途中接到臺風警報,臺風中心正以60海里/小時的速度由南向北移動,距臺風中心20海里的圓形區域(包括邊界)都屬于臺風區,當輪船到A處時,測得臺風中心移到位于點A正南方向的B處,且AB=40海里.
(1)若輪船以原方向、原速度繼續航行:
①船長發現,當臺風中心到達A處時,輪船肯定受影響,為什么?
②求輪船從A點出發到最初遇到臺風的時間;
(2)若輪船在A處迅速改變航線,向北偏東60°的方向的避風港以30海里/小時的速度駛去,輪船還會不會受到影響?若會,試求輪船最初遇到臺風的時間;若不會,請說明理由.

【答案】(1)①會受影響,理由見解析;②輪船從A點出發到最初遇到臺風的時間是![]() 小時;(2)輪船從A點出發到最初遇到臺風的時間是
小時;(2)輪船從A點出發到最初遇到臺風的時間是![]() 小時.
小時.
【解析】試題分析:(1)①求出當臺風中心到達A處時,所用時間,進而求出輪船此時駛離A處距離,比較即可;
②當輪船在t小時后到達A1時,最初遇到臺風,此時臺風中心到達B1,進而表示出各線段長,再利用勾股定理求出即可;
(2)當輪船在m時后到達A2時,最初遇到臺風,此時臺風中心到達B2,進而得出A2B2=20,A2A=30m,AB2=60m-40,作A2E⊥AB2,垂足為E,則A2E=15![]() m,AE=15m,EB2=AE-AB2,再利用勾股定理求出即可.
m,AE=15m,EB2=AE-AB2,再利用勾股定理求出即可.
試題解析:(1)①會受影響,
當臺風中心到達A處時,用時: ![]() (小時),
(小時),
則輪船此時駛離A處:30×![]() =20(海里),因此輪船肯定受影響;
=20(海里),因此輪船肯定受影響;
②如圖1,若輪船在t小時后到達A1時,最初遇到臺風,此時臺風中心到達B1,
則A1B1=20海里,A1A=30t,AB1=40﹣60t,
由勾股定理知,(30t)2+(40﹣60t)2=202,
解得:t1=![]() ,t2=
,t2=![]() ,
,
則輪船從A點出發到最初遇到臺風的時間是![]() 小時;
小時;
(2)會,理由:如圖2,若輪船在m時后到達A2時,最初遇到臺風,此時臺風中心到達B2,則A2B2=20,A2A=30m,AB2=60m﹣40,作A2E⊥AB2,垂足為E,則A2E=30m ×sin60°=15![]()
m,AE=15m,EB2=AE﹣AB2=15m﹣(60m﹣40)=40﹣45m,
由勾股定理得:(15![]() m)2+(40﹣45m)2=202,
m)2+(40﹣45m)2=202,
解得:m1=m2=![]() ,
,
則輪船從A點出發到最初遇到臺風的時間是![]() 小時.
小時.


科目:初中數學 來源: 題型:
【題目】已知拋物線y=x2+kx+2k﹣4
(1)當k=2時,求出此拋物線的頂點坐標;
(2)求證:無論k為任何實數,拋物線都與x軸有交點,且經過x軸一定點;
(3)已知拋物線與x軸交于A(x1,0)、B(x2,0)兩點(A在B的左邊),|x1|<|x2|,與y軸交于C點,且S△ABC=15.問:過A,B,C三點的圓與該拋物線是否有第四個交點?試說明理由.如果有,求出其坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
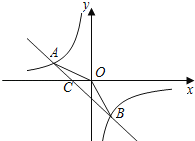
【題目】如圖,在平面直角坐標系xOy中,若點A(﹣2,n),B(1,﹣2)是一次函數y=kx+b的圖象和反比例函數y=![]() 的圖象的兩個交點.
的圖象的兩個交點.
(1)求反比例函數和一次函數的解析式;
(2)求直線AB與x軸的交點C的坐標;
(3)求點O到直線AB的距離.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分10分)閱讀下列材料:
(1)關于x的方程x2-3x+1=0(x≠0)方程兩邊同時乘以![]() 得:
得: ![]() 即
即![]() ,
, ![]() ,
,
(2)a3+b3=(a+b)(a2-ab+b2);a3-b3=(a-b)(a2+ab+b2).
根據以上材料,解答下列問題:
(1)x2-4x+1=0(x≠0),則![]() = ______ ,
= ______ , ![]() = ______ ,
= ______ , ![]() = ______ ;
= ______ ;
(2)2x2-7x+2=0(x≠0),求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com