
【題目】如圖,拋物線y=-![]() x2+bx+c,與
x2+bx+c,與![]() 軸交于點(diǎn)A和點(diǎn)B,與y軸交于點(diǎn)C,點(diǎn)B坐標(biāo)為(6,0),點(diǎn)C坐標(biāo)為(0,6),點(diǎn)D是拋物線的頂點(diǎn),過(guò)點(diǎn)D作x軸的垂線,垂足為E,連接BD.
軸交于點(diǎn)A和點(diǎn)B,與y軸交于點(diǎn)C,點(diǎn)B坐標(biāo)為(6,0),點(diǎn)C坐標(biāo)為(0,6),點(diǎn)D是拋物線的頂點(diǎn),過(guò)點(diǎn)D作x軸的垂線,垂足為E,連接BD.
(Ⅰ)求拋物線的解析式及點(diǎn)D的坐標(biāo);
(Ⅱ)點(diǎn)![]() 是拋物線上的動(dòng)點(diǎn),當(dāng)
是拋物線上的動(dòng)點(diǎn),當(dāng)![]() 時(shí),求點(diǎn)F坐標(biāo);
時(shí),求點(diǎn)F坐標(biāo);
(Ⅲ)若點(diǎn)P是x軸上方拋物線上的動(dòng)點(diǎn),以PB為邊作正方形PBFG,隨著點(diǎn)P的運(yùn)動(dòng),正方形的大小、位置也隨著改變,當(dāng)頂點(diǎn)F或G恰好落在y軸上時(shí),請(qǐng)直接寫(xiě)出點(diǎn)P的橫坐標(biāo).

【答案】(Ⅰ)y=-![]() x2+2x+6;
x2+2x+6;![]() ;(Ⅱ)
;(Ⅱ)![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() 或
或![]() ;(Ⅲ)點(diǎn)
;(Ⅲ)點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 或4或0.
或4或0.
【解析】
(Ⅰ)把B、C坐標(biāo)代入y=-![]() x2+bx+c,解方程組求出b、c的值即可得拋物線解析式,把解析式變形為頂點(diǎn)式可得D點(diǎn)坐標(biāo);(Ⅱ)過(guò)F作FG⊥x軸于點(diǎn)G,設(shè)F點(diǎn)坐標(biāo)為
x2+bx+c,解方程組求出b、c的值即可得拋物線解析式,把解析式變形為頂點(diǎn)式可得D點(diǎn)坐標(biāo);(Ⅱ)過(guò)F作FG⊥x軸于點(diǎn)G,設(shè)F點(diǎn)坐標(biāo)為![]() ,利用△FBG∽△BDE,由相似三角形的性質(zhì)可得到關(guān)于F點(diǎn)坐標(biāo)的方程,即可求得F點(diǎn)的坐標(biāo);(Ⅲ)設(shè)
,利用△FBG∽△BDE,由相似三角形的性質(zhì)可得到關(guān)于F點(diǎn)坐標(biāo)的方程,即可求得F點(diǎn)的坐標(biāo);(Ⅲ)設(shè)![]() ,分G在y軸上、F在y軸上、F在y軸上,P與C重合三種情況討論,根據(jù)正方形的性質(zhì)得出m的方程,求出m的值即可得P點(diǎn)橫坐標(biāo).
,分G在y軸上、F在y軸上、F在y軸上,P與C重合三種情況討論,根據(jù)正方形的性質(zhì)得出m的方程,求出m的值即可得P點(diǎn)橫坐標(biāo).
(Ⅰ)把點(diǎn)![]() 坐標(biāo)為(6,0),點(diǎn)
坐標(biāo)為(6,0),點(diǎn)![]() 坐標(biāo)為(0,6)代入拋物線y=-
坐標(biāo)為(0,6)代入拋物線y=-![]() x2+bx+c
x2+bx+c
得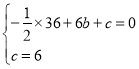 ,解得
,解得![]() .
.
∴![]() ,
,
∴![]() .
.
(Ⅱ)如圖1,過(guò)![]() 作
作![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,
,
設(shè)![]() ,則
,則![]()
∵![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∴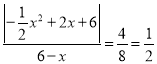 ,
,
當(dāng)點(diǎn)![]() 在
在![]() 軸上方時(shí),有
軸上方時(shí),有![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
此時(shí)![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() .
.
當(dāng)點(diǎn)![]() 在
在![]() 軸下方時(shí),有
軸下方時(shí),有![]() ,解得
,解得![]() 或
或![]() (舍去),
(舍去),
此時(shí)![]() 點(diǎn)坐標(biāo)為
點(diǎn)坐標(biāo)為![]() .
.
綜上可知![]() 點(diǎn)的坐標(biāo)為
點(diǎn)的坐標(biāo)為![]() 或
或![]() .
.
(Ⅲ)設(shè)![]() ,有三種情況:
,有三種情況:
①如圖2,當(dāng)![]() 在
在![]() 軸上時(shí),過(guò)P作
軸上時(shí),過(guò)P作![]() 軸于
軸于![]() ,作PM⊥x軸于
,作PM⊥x軸于![]() ,
,
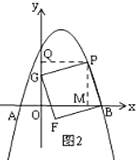
∵四邊形![]() 是正方形,
是正方形,
∴![]() .
.
∵![]() ,
,![]() ,
,
∴![]() ≌△PMB,
≌△PMB,
∴![]() .
.
即![]() ,解得
,解得![]() ,
,![]() (舍).
(舍).
∴![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() .
.
②當(dāng)![]() 在
在![]() 軸上時(shí),如圖3,過(guò)
軸上時(shí),如圖3,過(guò)![]() 作PM⊥x軸于M,
作PM⊥x軸于M,
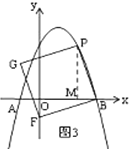
同理得:△PMB≌![]() ,
,
∴OB=PM=6.
即![]() ,解得:
,解得:![]() (舍),
(舍),![]() .
.
∴![]() 的橫坐標(biāo)為4.
的橫坐標(biāo)為4.
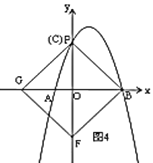
③當(dāng)![]() 在
在![]() 軸上時(shí),如圖4,此時(shí)
軸上時(shí),如圖4,此時(shí)![]() 與
與![]() 重合,此時(shí)
重合,此時(shí)![]() 的橫坐標(biāo)為0.
的橫坐標(biāo)為0.
綜上所述,點(diǎn)![]() 的橫坐標(biāo)為
的橫坐標(biāo)為![]() 或4或0.
或4或0.



| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】某商場(chǎng)的運(yùn)動(dòng)服裝專柜,對(duì)![]() 兩種品牌的遠(yuǎn)動(dòng)服分兩次采購(gòu)試銷(xiāo)后,效益可觀,計(jì)劃繼續(xù)采購(gòu)進(jìn)行銷(xiāo)售.已知這兩種服裝過(guò)去兩次的進(jìn)貨情況如下表.
兩種品牌的遠(yuǎn)動(dòng)服分兩次采購(gòu)試銷(xiāo)后,效益可觀,計(jì)劃繼續(xù)采購(gòu)進(jìn)行銷(xiāo)售.已知這兩種服裝過(guò)去兩次的進(jìn)貨情況如下表.
第一次 | 第二次 | |
| 20 | 30 |
| 30 | 40 |
累計(jì)采購(gòu)款/元 | 10200 | 14400 |
(1)問(wèn)![]() 兩種品牌運(yùn)動(dòng)服的進(jìn)貨單價(jià)各是多少元?
兩種品牌運(yùn)動(dòng)服的進(jìn)貨單價(jià)各是多少元?
(2)由于![]() 品牌運(yùn)動(dòng)服的銷(xiāo)量明顯好于
品牌運(yùn)動(dòng)服的銷(xiāo)量明顯好于![]() 品牌,商家決定采購(gòu)
品牌,商家決定采購(gòu)![]() 品牌的件數(shù)比
品牌的件數(shù)比![]() 品牌件數(shù)的
品牌件數(shù)的![]() 倍多5件,在采購(gòu)總價(jià)不超過(guò)21300元的情況下,最多能購(gòu)進(jìn)多少件
倍多5件,在采購(gòu)總價(jià)不超過(guò)21300元的情況下,最多能購(gòu)進(jìn)多少件![]() 品牌運(yùn)動(dòng)服?
品牌運(yùn)動(dòng)服?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
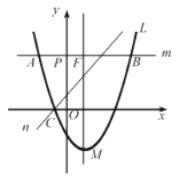
【題目】如圖,拋物線![]() (
(![]() ,
,![]() 為常數(shù)且
為常數(shù)且![]() )經(jīng)過(guò)點(diǎn)
)經(jīng)過(guò)點(diǎn)![]() ,頂點(diǎn)為
,頂點(diǎn)為![]() ,經(jīng)過(guò)點(diǎn)
,經(jīng)過(guò)點(diǎn)![]() 的直線
的直線![]() 與
與![]() 軸平行,且
軸平行,且![]() 與
與![]() 交于點(diǎn)
交于點(diǎn)![]() ,
,![]() (
(![]() 在
在![]() 的右側(cè)),與
的右側(cè)),與![]() 的對(duì)稱軸交于點(diǎn)
的對(duì)稱軸交于點(diǎn)![]() ,直線
,直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() .
.
(1)用![]() 表示
表示![]() 及點(diǎn)
及點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
(2)![]() 的值是否是定值?若是,請(qǐng)求出這個(gè)定值;若不是,請(qǐng)說(shuō)明理由;
的值是否是定值?若是,請(qǐng)求出這個(gè)定值;若不是,請(qǐng)說(shuō)明理由;
(3)當(dāng)直線![]() 經(jīng)過(guò)點(diǎn)
經(jīng)過(guò)點(diǎn)![]() 時(shí),求
時(shí),求![]() 的值及點(diǎn)
的值及點(diǎn)![]() ,
,![]() 的坐標(biāo);
的坐標(biāo);
(4)當(dāng)![]() 時(shí),設(shè)
時(shí),設(shè)![]() 的外心為點(diǎn)
的外心為點(diǎn)![]() ,則
,則
①求點(diǎn)![]() 的坐標(biāo);
的坐標(biāo);
②若點(diǎn)![]() 在
在![]() 的對(duì)稱軸上,其縱坐標(biāo)為
的對(duì)稱軸上,其縱坐標(biāo)為![]() ,且滿足
,且滿足![]() ,直接寫(xiě)出
,直接寫(xiě)出![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
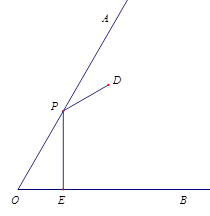
【題目】如圖,已知∠AOB=60°,點(diǎn)P為射線OA上的一個(gè)動(dòng)點(diǎn),過(guò)點(diǎn)P作PE⊥OB,交OB 于點(diǎn)E,點(diǎn)D在∠AOB內(nèi),且滿足∠DPA=∠OPE,DP+PE=6.
(1)當(dāng)DP=PE時(shí),求DE的長(zhǎng);
(2)在點(diǎn)P的運(yùn)動(dòng)過(guò)程中,請(qǐng)判斷是否存在一個(gè)定點(diǎn)M,使得![]() 的值不變?并證明你的判斷.
的值不變?并證明你的判斷.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
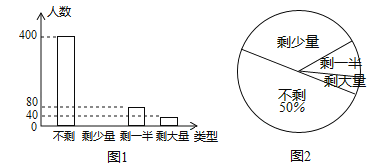
【題目】某企業(yè)工會(huì)開(kāi)展“一周工作量完成情況”調(diào)查活動(dòng),隨機(jī)調(diào)查了部分員工一周的工作量剩余情況,并將調(diào)查結(jié)果統(tǒng)計(jì)后繪制成如圖 1 和圖 2 所示的不完整統(tǒng)計(jì)圖 .
(1) 被調(diào)查員工的人數(shù)為 人:
(2) 把條形統(tǒng)計(jì)圖補(bǔ)充完整;
(3) 若該企業(yè)有員工 10000 人,請(qǐng)估計(jì)該企業(yè)某周的工作量完成情況為“剩少量”的員工有多少人?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
【題目】如圖,![]() 是⊙
是⊙![]() 的直徑,弦
的直徑,弦![]() 于
于![]() ,點(diǎn)
,點(diǎn)![]() 在弧
在弧![]() 上(不含端點(diǎn)
上(不含端點(diǎn)![]() ), 連接
), 連接![]()
![]()
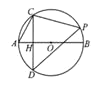
(1)圖中有無(wú)和![]() 相等的線段,并證明你的結(jié)論.
相等的線段,并證明你的結(jié)論.
(2)求![]() 的值。
的值。
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
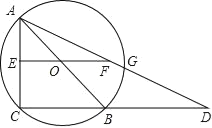
【題目】如圖,已知AB是⊙O的直徑,C是⊙O上的點(diǎn),連接AC、CB,過(guò)O作EO∥CB并延長(zhǎng)EO到F,使EO=FO,連接AF并延長(zhǎng),AF與CB的延長(zhǎng)線交于D.求證:AE2=FGFD.
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
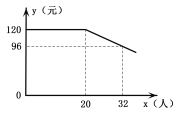
【題目】隨著人們生活水平的提高,短途旅行日趨火爆.我市某旅行社推出“遼陽(yáng)—葫蘆島海濱觀光一日游”項(xiàng)目,團(tuán)隊(duì)人均報(bào)名費(fèi)用y(元)與團(tuán)隊(duì)報(bào)名人數(shù)x(人)之間的函數(shù)關(guān)系如圖所示,旅行社規(guī)定團(tuán)隊(duì)人均報(bào)名費(fèi)用不能低于88元.旅行社收到的團(tuán)隊(duì)總報(bào)名費(fèi)用為w(元).
(1)直接寫(xiě)出當(dāng)x≥20時(shí),y與x之間的函數(shù)關(guān)系式及自變量x的取值范圍;
(2)兒童節(jié)當(dāng)天旅行社收到某個(gè)團(tuán)隊(duì)的總報(bào)名費(fèi)為3000元,報(bào)名旅游的人數(shù)是多少?
(3)當(dāng)一個(gè)團(tuán)隊(duì)有多少人報(bào)名時(shí),旅行社收到的總報(bào)名費(fèi)最多?最多總報(bào)名費(fèi)是多少元?
查看答案和解析>>
科目:初中數(shù)學(xué) 來(lái)源: 題型:
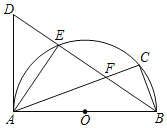
【題目】如圖,以AB為直徑作半圓O,點(diǎn)C是半圓上一點(diǎn),∠ABC的平分線交⊙O于E,D為BE延長(zhǎng)線上一點(diǎn),且DE=FE.
(1)求證:AD為⊙O切線;
(2)若AB=20,tan∠EBA=![]() ,求BC的長(zhǎng).
,求BC的長(zhǎng).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com