
【題目】已知二次函數y=ax2+bx+c(c≠4a),其圖象L經過點A(-2,0).
(1)求證:b2-4ac>0;
(2)若點B(-![]() ,b+3)在圖象L上,求b的值;
,b+3)在圖象L上,求b的值;
(3)在(2)的條件下,若圖象L的對稱軸為直線x=3,且經過點C(6,-8),點D(0,n)在y軸負半軸上,直線BD與OC相交于點E,當△ODE為等腰三角形時,求n的值.
【答案】(1)證明見解析;(2)-3;(3)![]() 或
或![]()
【解析】試題分析:(1)將點A坐標代入函數解析式中,得b=2a+ ![]() c,再代入b2-4ac中得,b2-4ac=(2a-
c,再代入b2-4ac中得,b2-4ac=(2a-![]() c)2,由c≠4a得2a-
c)2,由c≠4a得2a-![]() c≠0,所以(2a-
c≠0,所以(2a-![]() c)2>0,即b2-4ac>0. (2)將點B的坐標代入函數解析式中得:
c)2>0,即b2-4ac>0. (2)將點B的坐標代入函數解析式中得: ![]() ,由4a-2b+c=0,所以b+3=0,解得b=-3;(3)由題意,得
,由4a-2b+c=0,所以b+3=0,解得b=-3;(3)由題意,得![]() ,且36a-18+c=-8,解得a=
,且36a-18+c=-8,解得a=![]() ,c=-8.所以圖象L的解析式為y=
,c=-8.所以圖象L的解析式為y=![]() x2-3x-8. 設OC與對稱軸交于點Q,圖象L與y軸相交于點P,則Q(3,-4),P(0,-8),OQ=PQ=5.分兩種情況:①當OD=OE時,②當EO=ED時,討論求值即可;
x2-3x-8. 設OC與對稱軸交于點Q,圖象L與y軸相交于點P,則Q(3,-4),P(0,-8),OQ=PQ=5.分兩種情況:①當OD=OE時,②當EO=ED時,討論求值即可;
試題解析:
(1)證明:
由題意,得4a-2b+c=0,
∴b=2a+![]() c.
c.
∴b2-4ac=(2a+![]() c)2-4ac=(2a-
c)2-4ac=(2a-![]() c)2.
c)2.
∵c≠4a,
∴2a-![]() c≠0,
c≠0,
∴(2a-![]() c)2>0,即b2-4ac>0.
c)2>0,即b2-4ac>0.
(2)解:∵點B(-![]() ,b+3)在圖象L上,
,b+3)在圖象L上,
∴![]() ,整理,得
,整理,得![]() .
.
∵4a-2b+c=0,
∴b+3=0,解得b=-3.
(3)解:由題意,得![]() ,且36a-18+c=-8,解得a=
,且36a-18+c=-8,解得a=![]() ,c=-8.
,c=-8.
∴圖象L的解析式為y=![]() x2-3x-8.
x2-3x-8.
設OC與對稱軸交于點Q,圖象L與y軸相交于點P,
則Q(3,-4),P(0,-8),OQ=PQ=5.
分兩種情況:
①當OD=OE時,如圖1,
過點Q作直線MQ∥DB,交y軸于點M,交x軸于點H,
則![]() ,
,
∴OM=OQ=5.
∴點M的坐標為(0,-5).
設直線MQ的解析式為![]() .
.
∴![]() ,解得
,解得![]() .
.
∴MQ的解析式為![]() .易得點H(15,0).
.易得點H(15,0).
又∵MH∥DB, ![]() .
.
即![]() ,
,
∴![]() .
.
②當EO=ED時,如圖2,
∵OQ=PQ,
∴![]() 1=
1=![]() 2,又EO=ED,
2,又EO=ED,
∴![]() 1=
1=![]() 3.
3.
∴![]() 2=
2=![]() 3,
3,
∴PQ∥DB.
設直線PQ交于點N,其函數表達式為![]()
∴![]() ,解得
,解得![]() .
.
∴PQ的解析式為![]() .
.
∴點N的坐標為(6,0).
∵PN∥DB,
∴![]() ,
,
∴![]() ,解得
,解得![]() .
.

綜上所述,當△ODE是等腰三角形時,n的值為![]() 或
或![]() .
.


 優等生題庫系列答案
優等生題庫系列答案科目:初中數學 來源: 題型:
【題目】已知二次函數![]() 與一次函數
與一次函數![]() ,令W=
,令W=![]() .
.
(1)若![]() 、
、![]() 的函數圖像交于x軸上的同一點.
的函數圖像交于x軸上的同一點.
①求![]() 的值;
的值;
②當![]() 為何值時,W的值最小,試求出該最小值;
為何值時,W的值最小,試求出該最小值;
(2)當![]() 時,W隨x的增大而減小.
時,W隨x的增大而減小.
①求![]() 的取值范圍;
的取值范圍;
②求證: ![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】不透明的盒中裝著大小、外形、質地一樣的紅色、黑色、白色的乒乓球共20個,通過多次摸球實驗后發現其中摸到紅色、黑色球的概率穩定在5%和15%,則盒子中白色球的個數很可能是__________個.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】冥王星圍繞太陽公轉的軌道半徑長度約為5900000000千米,5900000000用科學記數法表示是( )
A. 5.9×1010B. 5.9×109C. 59×108D. 0.59×1010
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,正確的命題個數為( )
①所有的等腰三角形都相似;
②有一對銳角相等的兩個直角三角形相似;
③所有的正方形都相似;
④四個角對應相等的兩個梯形相似.
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在等腰Rt△ABC中,∠ACB=90°,AC=CB,F是AB邊上的中點,點D、E分別在AC、BC邊上運動,且始終保持AD=CE.連接DE、DF、EF. 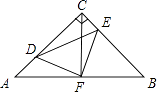
(1)求證:△ADF≌△CEF;
(2)試證明△DFE是等腰直角三角形.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小穎在二次函數y=2x2+4x+5的圖象上,依橫坐標找到三點(﹣1,y1),(2,y2),(﹣3,y3),則你認為y1 , y2 , y3的大小關系應為 .
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com