【題目】如圖，在平面直角坐標系中，
的四個頂點分別為
，
，
，
．
（1）作
，使它與關于原點
成中心對稱．
（2）作的兩條對角線的交點
關于
軸的對稱點
，點的坐標為_______．
（3）若將點向上平移
個單位，使其落在內部(不包括邊界)，則的取值范圍是_______．
孟建平名校考卷系列答案科目：初中數學 來源： 題型：
【題目】探索與拓展應用，
已知△ABC為等邊三角形，點D為直線BC上的一動點（點D不與B、C重合），以AD為邊作菱形ADEF（A、D、E、F按逆時針排列），使∠DAF=60°，連接CF．
（1）如圖1，當點D在邊BC上時，求證：①BD=CF；②AC=CF+CD；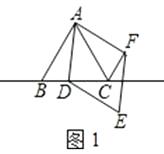
（2）如圖2，當點D在邊BC的延長線上且其他條件不變時，結論AC=CF+CD是否成立？若不成立，請寫出AC、CF、CD之間存在的數量關系，并說明理由；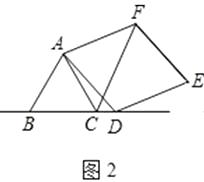
（3）如圖3，當點D在邊CB的延長線上且其他條件不變時，補全圖形，并直接寫出AC、CF、CD之間存在的數量關系．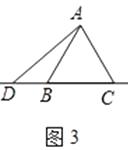
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】一慢車和一快車沿相同路線從A地到B地，所行的路程與時間的圖象如圖所示，試根據圖象，回答下列問題：
(1)慢車比快車早出發______小時，快車追上慢車時行駛了_____千米，快車比慢車早______小時到達B地；
(2)求慢車、快車的速度；
(3)快車追上慢車需幾個小時？
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，已知AB∥DC，AE平分∠BAD，CD與AE相交于點F，∠CFE＝∠E.試說明AD∥BC.完成推理過程：
∵AB∥DC( )，
∴∠1＝∠CFE( )．
∵AE平分∠BAD( )，
∴∠1＝ ( )．
∵∠CFE＝∠E( ),
∴∠2＝ (等量代換)，
∴AD∥ ( )．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】請填空，完成下面的證明，并注明理由．
如圖，
，
，BE平分
，DF平分
．
求證：
．
證明：∵，（已知）
∴
．（_________）
∵，（已知）
∴__________
．（兩直線平行，同旁內角互補）
∴
．（_________）
∵
，（已知）
∴
．（_________）
同理，
．
∴________=
．
∵，（已知）
∴
．（兩直線平行，內錯角相等）
∴
．
∴
．（__________）
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，多邊形OABCDE的頂點坐標分別是O（0，0）、A（0，6）、B（4，6）、C（4，4）、D（6，4），E（6，0），若直線L經過點M（2，3），且將多邊形OABCDE分割成面積相等的兩部分，則直線L的函數表達式是 
查看答案和解析>>
科目：初中數學 來源： 題型：
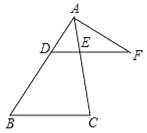
【題目】如圖，在△ABC中，點D是AB邊上一點，過點D作DE∥BC，交AC于E，點F是DE延長線上一點，聯結AF．
（1）如果
，DE=6，求邊BC的長；
（2）如果∠FAE=∠B，FA=6，FE=4，求DF的長．
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】大小兩種貨車運送360臺機械設備，有三種運輸方案．
方案一：設備的
用大貨車運送，其余用小貨車運送，需要貨車27輛．
方案二：設備的
用大貨車運送，其余用小貨車運送，需要貨車28輛．
方案三：設備的
用大貨車運送，其余用小貨車運送，需要貨車26輛．
（1）每輛大、小貨車各可運送多少臺機械設備？
（2）如果大貨車運費比小貨車高m%（m>0），請你從中選擇一種方案，使得運費最低，并說明理由．
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
