
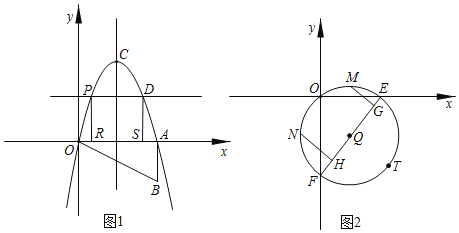
【題目】如圖,Rt△OAB如圖所示放置在平面直角坐標系中,直角邊OA與x軸重合,∠OAB=90°,OA=4,AB=2,把Rt△OAB繞點O逆針旋轉90°,點B旋轉到點C的位置,一條拋物找正好經過點O,C,A三點.
(1)求該拋物線的解析式;
(2)在x軸上方的拋物線上有一動點P,過點P作x軸的平行線交拋物線于點D,分別過點P,點D作x軸的垂線,交x軸于R,S兩點,問:四邊形PRSD的周長是否有最大值?如果有,請求出最值,并寫出解答過程;如果沒有,請說明理由.
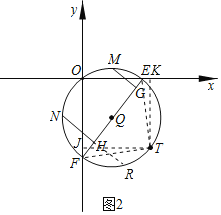
(3)如圖2,把點B向下平移兩個單位得到點T,過O,T兩點作⊙Q交x軸,y軸于E,F兩點,若M、N分別為弧![]() 、
、![]() 的中點,作MG⊥EF,NH⊥EF,垂足為G、H,試求MG+NH的值.
的中點,作MG⊥EF,NH⊥EF,垂足為G、H,試求MG+NH的值.
【答案】(1)y=-x2+4x;(2)當a=1時,矩形PEFM的周長有最大值10;(3)MG+NH=4.
【解析】
(1)根據旋轉變換的性質求出點C的坐標,利用待定系數法求出拋物線的解析式;
(2)設點P的坐標為P(a,-a2+4a),根據拋物線的對稱性求出RS,根據二次函數的性質計算;
(3)作TK⊥x軸于K,TJ⊥y軸于J,連接TF,TE,延長NH交⊙Q于R,證明△ETK≌△FTJ,根據全等三角形的性質得到EK=FJ,得到OE+OF=8,根據垂徑定理得到NH=NR=![]() OF,計算即可.
OF,計算即可.
解:(1)設y=ax2+bx+c,
∵OA=4,AB=2,
∴點A的坐標為(4,0),點B的坐標為(4,-2),
△AOB繞點O逆時針旋轉90°,點B旋轉到點C的位置,
∴點C的坐標為(2,4),
則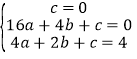
解得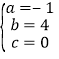 .
.
所以拋物線的解析式為y=-x2+4x;
(2)有最大值.
理由如下:設點P的坐標為P(a,-a2+4a),PR=DS=-a2+4a,
由拋物線的對稱性知OR=AS,RS=PD=4-2a,
矩形PRSD的周長=2[4-2a+(-a2+4a)]=-2(a-1)2+10,
所以當a=1時,矩形PEFM的周長有最大值10;
(3)作TK⊥x軸于K,TJ⊥y軸于J,連接TF,TE,延長NH交⊙Q于R,
由題意得,點T的坐標為(4,-4,),即TJ=TK=4,
∴點T在∠EOF的平分線上,
∴![]() =
=![]()
∴TE=TF,
在Rt△TKE和Rt△TJF中,
![]() ,
,
∴△ETK≌△FTJ(HL),
∴EK=FJ,∠EOF=∠KTJ=90°,
∴OE+OF=OK-EK+OJ+FJ=OJ+OK=8,
∴EF為⊙Q的直徑,
∴![]() =
=![]() ,
,
∵N為![]() 的中點,
的中點,
∴![]() =
=![]() ,
,
∴![]() =
=![]() ,
,
∴NR=OF,
∴NH=NR=![]() OF,
OF,
同理MG=![]() OE,
OE,
∴MG+NH=![]() (OE+OF)=
(OE+OF)=![]() ×8=4.
×8=4.


科目:初中數學 來源: 題型:
【題目】(問題解決)
一節數學課上,老師提出了這樣一個問題:如圖1,點P是正方形ABCD內一點,PA=1,PB=2,PC=3.你能求出∠APB的度數嗎?
小明通過觀察、分析、思考,形成了如下思路:
思路一:將△BPC繞點B逆時針旋轉90°,得到△BP′A,連接PP′,求出∠APB的度數;
思路二:將△APB繞點B順時針旋轉90°,得到△CP'B,連接PP′,求出∠APB的度數.
請參考小明的思路,任選一種寫出完整的解答過程.
(類比探究)
如圖2,若點P是正方形ABCD外一點,PA=3,PB=1,PC=![]() ,求∠APB的度數.
,求∠APB的度數.

查看答案和解析>>
科目:初中數學 來源: 題型:
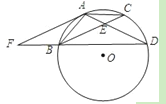
【題目】如圖,點A,B,C,D在⊙O上,AB=AC,AD與BC相交于點E,AE=![]() ED,延長DB到點F,使FB=
ED,延長DB到點F,使FB=![]() BD,連接AF.
BD,連接AF.
(1)證明:△BDE∽△FDA;
(2)試判斷直線AF與⊙O的位置關系,并給出證明.
查看答案和解析>>
科目:初中數學 來源: 題型:
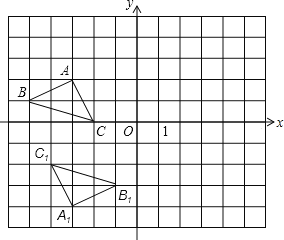
【題目】如圖,在平面直角坐標系中,已知△ABC的三個頂點坐標分別是A(1,1),B(4,1),C(3,3).
(1)將△ABC向下平移5個單位后得到△A1B1C1,請畫出△A1B1C1;
(2)將△ABC繞原點O逆時針旋轉90°后得到△A2B2C2,請畫出△A2B2C2;
(3)判斷以O,A1,B為頂點的三角形的形狀.(無須說明理由)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列命題中,屬于假命題的是( )
A. 有一個銳角相等的兩個直角三角形一定相似
B. 對角線相等的菱形是正方形
C. 拋物線y=x2﹣20x+17的開口向上
D. 在一次拋擲圖釘的試驗中,若釘尖朝上的頻率為![]() ,釘尖朝下的概率為
,釘尖朝下的概率為![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,每個小正方形網格的邊長為1,![]() 和
和![]() 關于點
關于點![]() 成中心對稱.
成中心對稱.
(1)畫出對稱中心![]() ,并寫出點
,并寫出點![]() 的坐標______.
的坐標______.
(2)畫出![]() 繞點
繞點![]() 順時針旋轉
順時針旋轉![]() 后的
后的![]() ;連接
;連接![]() ,可求得線段
,可求得線段![]() 長為______.
長為______.
(3)畫出![]() 與關于點
與關于點![]() 成中心對稱的
成中心對稱的![]() ;連接
;連接![]() 、
、![]() ,則四邊形
,則四邊形![]() 是______;(填屬于哪一種特殊四邊形),它的面積是______.
是______;(填屬于哪一種特殊四邊形),它的面積是______.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知AB=8cm,小紅在作線段AB的垂直平分線時操作如下:分別以A和B為圓心,5cm的長為半徑畫弧,兩弧相交于C、D,則直線CD即為所求,根據此種作圖方法所得到的四邊形ADBC的面積是( )
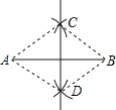
A.12cm2B.24cm2C.36cm2D.48cm2
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,若干個全等的正五邊形排成環狀,圖中所示的是前3個正五邊形,要完成這一圓環還需正五邊形的個數為( )
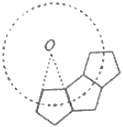
A. 10 B. 9 C. 8 D. 7
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com