
【題目】某班同學積極響應“陽光體育工程”的號召,利用課外活動時間積極參加體育鍛煉,每位同學從長跑、籃球、鉛球、立定跳遠中選一項進行訓練,訓練前后郗進行了測試.現將項目選擇情況及訓練前后籃球定時定點投測試成績整理作出如下統計圖表.
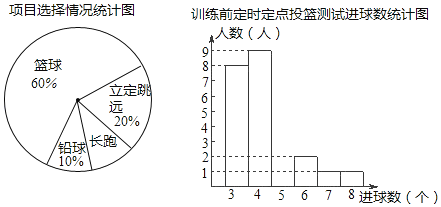
訓練后籃球定時定點投籃測試進球數統計表:
進球數(個) | 8 | 7 | 6 | 5 | 4 | 3 |
人數 | 2 | 1 | 4 | 7 | 8 | 2 |
請你根據圖表中的信息回答下列問題
(1)送擇長跑訓練的人數占全班人數的百分比是 ,該班共有同學 人;
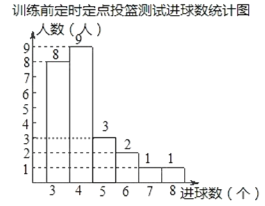
(2)直接補全“訓練前籃球定時定點投測試進球數統計圖”;
(3)若全區共有該年級學生4000人,請估計參加訓練后籃球定時定點投籃進球數達到6個以上(包含6個)多少人?
【答案】(1)10%,40;(2)見解析;(3)大約有700人
【解析】
(1)從扇形統計圖中,從1中減去其它各個項目占比即可,從訓練后的進球數的統計表中,可以計算出選擇“籃球”的人數為24人,從扇形統計圖中可得選擇“籃球”占班級人數的60%,可求出班級人數,
(2)求出訓練前進3個球的人數,即可補全訓練前的條形統計圖,
(3)樣本估計總體,訓練后,進球在6個及以上的占選擇“籃球”人數的![]() ,而選擇“籃球”的人數占總人數的60%,于是可以先求出選擇“籃球”的人數,再求出進球在6個及以上的人數.
,而選擇“籃球”的人數占總人數的60%,于是可以先求出選擇“籃球”的人數,再求出進球在6個及以上的人數.
解:(1)1﹣60%﹣20%﹣10%=10%,
(2+1+4+7+8+2)÷60%=40人,
故答案為:10%,40;
(2)訓練前進3個球的人數為:(2+1+4+7+8+2)﹣(9+8+2+1+1)=34﹣21=3人,
補全的條形統計圖如圖所示:
(3)4000×60%×![]() =700人,
=700人,
答:訓練后籃球定時定點投籃進球數達到6個以上(包含6個)大約有700人.


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
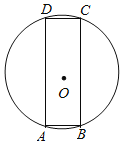
【題目】如圖,四邊形ABCD是⊙O的內接矩形,將矩形ABCD沿著直線BC翻折,點A、點D的對應點分別為A′、D′,如果直線A′D′與⊙O相切,那么![]() 的值為_____.
的值為_____.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲、乙兩校各選派10名學生參加“美麗泰州鄉土風情知識”大賽預賽.各參賽選手的成績如下:
甲校:93,98,89,93, 95,96, 93,96,98, 99;
乙校:93,94,88,91,92,93,100, 98,98,93.
通過整理,得到數據分析表如下:
學校 | 最高分 | 平均分 | 中位數 | 眾數 | 方差 |
甲校 | 99 | a | 95.5 | 93 | 8.4 |
乙校 | 100 | 94 | b | 93 | c |
(1)填空:a = ,b = ;
(2)求出表中c的值,你認為哪所學校代表隊成績好?請寫出兩條你認為該隊成績好的理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,點E為矩形ABCD的邊BC長上的一點,作DF⊥AE于點F,且滿足DF=AB.下面結論:①△DEF≌△DEC;②S△ABE = S△ADF;③AF=AB;④BE=AF.其中正確的結論是( )
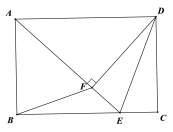
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】拋物線y=﹣x2+bx+c上部分點的橫坐標x,縱坐標y的對應值如下表所示:
x | … | ﹣2 | ﹣1 | 0 | 1 | 2 | … |
y | … | 0 | 4 | 6 | 6 | 4 | … |
從上表可知,下列說法中,錯誤的是( )
A. 拋物線于x軸的一個交點坐標為(﹣2,0)
B. 拋物線與y軸的交點坐標為(0,6)
C. 拋物線的對稱軸是直線x=0
D. 拋物線在對稱軸左側部分是上升的
查看答案和解析>>
科目:初中數學 來源: 題型:
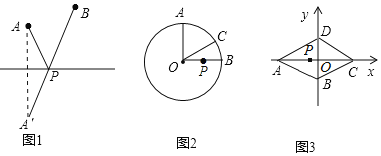
【題目】閱讀材料:“最值問題”是數學中的一類較具挑戰性的問題.其實,數學史上也有不少相關的故事,如下即為其中較為經典的一則:海倫是古希臘精通數學、物理的學者,相傳有位將軍曾向他請教一個問題﹣﹣如圖1,從A點出發,到筆直的河岸l去飲馬,然后再去B地,走什么樣的路線最短呢?海倫輕松地給出了答案:作點A關于直線l的對稱點A′,連接A′B交l于點P,則PA+PB=A′B 的值最小.
解答問題:
(1)如圖2,⊙O的半徑為2,點A、B、C在⊙O上,OA⊥OB,∠AOC=60°,P是OB上一動點,求PA+PC的最小值;
(2)如圖3,已知菱形ABCD的邊長為6,∠DAB=60°.將此菱形放置于平面直角坐標系中,各頂點恰好在坐標軸上.現有一動點P從點A出發,以每秒2個單位的速度,沿A→C的方向,向點C運動.當到達點C后,立即以相同的速度返回,返回途中,當運動到x軸上某一點M時,立即以每秒1個單位的速度,沿M→B的方向,向點B運動.當到達點B時,整個運動停止.
①為使點P能在最短的時間內到達點B處,則點M的位置應如何確定?
②在①的條件下,設點P的運動時間為t(s),△PAB的面積為S,在整個運動過程中,試求S與t之間的函數關系式,并指出自變量t的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(12分)如圖,在四邊形ABCD中,AD∥BC,AE=2EB,AD=2,BC=5,EF∥DC,交BC于點F,連接AF.
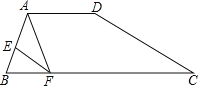
(1)求CF的長;
(2)若∠BFE=∠FAB,求AB的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(2017重慶A卷第11題)如圖,小王在長江邊某瞭望臺D處,測得江面上的漁船A的俯角為40°,若DE=3米,CE=2米,CE平行于江面AB,迎水坡BC的坡度i=1:0.75,坡長BC=10米,則此時AB的長約為( )(參考數據:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84).
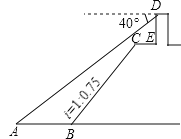
A. 5.1米 B. 6.3米 C. 7.1米 D. 9.2米
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com