
【題目】綜合題
(1)【問題提出】如圖1.△ABC是等邊三角形,點D在線段AB上.點E在直線BC上.且∠DEC=∠DCE.求證:BE=AD;
(2)【類比學習】如圖2.將條件“點D在線段AB上”改為“點D在線段AB的延長線上”,其他條件不變.判斷線段AB,BE,BD之間的數量關系,并說明理由.
(3)【擴展探究】如圖3.△ABC是等腰三角形,AB=AC,∠BAC=120°,點D在線段AB的反向延長線上,點E在直線BC上,且∠DEC=∠DCE,【類比學習】中的線段AB、BE、BD之間的數量關系是否還成立?若成立,請說明理由;若不成立,請直接寫出線段AB,BE,BD之間的數量.
【答案】
(1)證明:作DF∥BC交AC于F,如圖1所示:
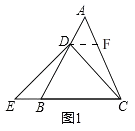
則∠ADF=∠ABC,∠AFD=∠ACB,∠FDC=∠DCE,
∵△ABC是等腰三角形,∠A=60°,
∴△ABC是等邊三角形,
∴∠ABC=∠ACB=60°,
∴∠DBE=120°,∠ADF=∠AFD=60°=∠A,
∴△ADF是等邊三角形,∠DFC=120°,
∴AD=DF,
∵∠DEC=∠DCE,
∴∠FDC=∠DEC,ED=CD,
在△DBE和△CFD中, 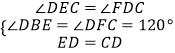 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD
(2)解:EB=AB+BD;理由如下:
作DF∥BC交AC的延長線于F,如圖2所示:
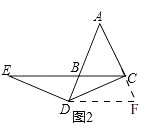
同(1)得:AD=DF,∠FDC=∠ECD,∠FDC=∠DEC,ED=CD,
又∵∠DBE=∠DFC=60°,
∴在△DBE和△CFD中, 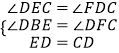 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,
∴EB=AD,
∴EB=AB+BD
(3)解: ![]() BE=3DB﹣3AB.
BE=3DB﹣3AB.
理由:作DF∥BC交CA的延長線于F,如圖3所示,
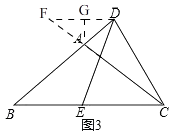
則∠ADF=∠ABC,∠AFD=∠ACB,∠FDC+∠DCE=180°,
∵△ABC是等腰三角形,
∴∠ABC=∠ACB,
∴∠ADF=∠AFD=∠ABC,
∵∠DEC=∠DCE,
∴DE=DC,∠FDC+∠DEC=180°,
∵∠DEC+∠DEB=180°,
∴∠FDC=∠DEB,
在△DBE和△CFD中, 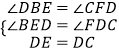 ,
,
∴△DBE≌△CFD(AAS),
∴EB=DF,DB=CF,
∵CF=AC+AF=AB+AF,
∴DB=AB+AF,
過點A作AG⊥DF于G,
∵AF=AD,
∴DF=2FG,
在Rt△AFG中,∠AFG=90°﹣∠FAG=90°﹣ ![]() ∠BAC=30°,
∠BAC=30°,
∴FG= ![]() AF,
AF,
∴EB=DF=2FG= ![]() AF,
AF,
∴AF= ![]() EB
EB
∴DB=AB+ ![]() BE,
BE,
即: ![]() BE=3DB﹣3AB.
BE=3DB﹣3AB.
【解析】(1)作DF∥BC交AC于F,首先證明△ABC是等邊三角形,然后再由AAS證明△DBE≌△CFD,得出EB=DF,即可得出結論;
(2)作DF∥BC交AC的延長線于F,首先證明△DBE≌△CFD,從而可得到EB=DF,即可得出結論;
(3)作DF∥BC交CA的延長線于F,首先證明△DBE≌△CFD,從而可得到EB=DF,再利用含30°的直角三角形的性質即可得出結論.


 寶貝計劃期末沖刺奪100分系列答案
寶貝計劃期末沖刺奪100分系列答案 能考試全能100分系列答案
能考試全能100分系列答案科目:初中數學 來源: 題型:
【題目】如圖有A、B、C三地依次在一條筆直的公路上,A、B兩地相距40km,一輛甲車以40km/h的速度從B地到C地;同時一輛乙車以80km/h的速度從B地開往A地,到達A地后,然后以120km/h的速度開往C地,兩車在各段內均勻速行駛,圖中線段EF與折線EMN分別表示甲、乙兩車距C地的路程y(千米)與行駛時間x(小時)之間的函數關系圖象.
(1)寫出點M的坐標為_______;點E的縱坐標的意義是________.
(2)請直接寫出n,b的值,并求出線段EF與MN的函數關系式;
(3)兩車出發幾小時后,乙車追上甲車?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為支援雅安災區,某學校計劃用“義捐義賣”活動中籌集的部分資金用于購買A,B兩種型號的學習用品共1000件,已知A型學習用品的單價為20元,B型學習用品的單價為30元.
(1)若購買這批學習用品用了26000元,則購買A,B兩種學習用品各多少件?
(2)若購買這批學習用品的錢不超過28000元,則最多購買B型學習用品多少件?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=4,BC=2,點D是邊AB上一點,CD將△ABC分成△ACD和△BCD,若△ACD是以AC為底的等腰三角形,且△BCD與△BAC相似,則CD的長為( )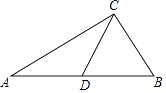
A.![]()
B.2
C.4 ![]() ﹣4
﹣4
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
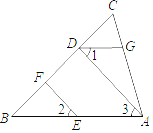
【題目】填寫下列空格完成證明:如圖, EF∥AD , 1 2 , BAC 70 ,求AGD .
解:∵ EF∥AD ,
∴ 2 .( )
∵ 1 2 ,
∴ 1 3.( )
∴ ∥ .( )
∴ BAC 180 .( )
∵ BAC 70 ,
∴ AGD .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在正方形ABCD中,連接BD,點O是BD的中點,若M,N是邊AD上的兩點,連接MO,NO,并分別延長交邊BC于兩點M′,N′,則圖中的全等三角形共有( )
A.2對
B.3對
C.4對
D.5對
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在△ABC 中,AB BC AC,∠A ∠B ∠C 60°.點 D、E 分別是邊 AC、AB 上的點(不與 A、B、C 重合),點 P 是平面內一動點.設∠PDC=∠1,∠PEB=∠2,∠DPE=∠α.
(1)若點 P 在邊 BC 上運動(不與點 B 和點 C 重合),如圖⑴所示,則∠1+∠2 .(用 α 的代數式表示)
(2)若點 P 在△ABC 的外部,如圖⑵所示,則∠α、∠1、∠2 之間有何關系?寫出你的結論,并說明理由.
(3)當點 P 在邊 BC 的延長線上運動時,試畫出相應圖形,并寫出∠α、∠1、∠2 之間的關系式.(不需要證明)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】幾何探究題
(1)發現:在平面內,若BC=a,AC=b,其中a>b.
當點A在線段BC上時(如圖1),線段AB的長取得最小值,最小值為 ;
當點A在線段BC延長線上時(如圖2),線段AB的長取得最大值,最大值為 .
(2)應用:點A為線段BC外一動點,如圖3,分別以AB、AC為邊,作等邊△ABD和等邊△ACE,連接CD、BE.
①證明:CD=BE;
②若BC=3,AC=1,則線段CD長度的最大值為 .
(3)拓展:如圖4,在平面直角坐標系中,點A的坐標為(2,0),點B的坐標為(5,0),點P為線AB外一動點,且PA=2,PM=PB,∠BPM=90°.請直接寫出線段AM長的最大值及此時點P的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在邊長為1的小正方形組成的方格紙中,若多邊形的每個頂點都在方格紙的格點(橫豎格子線的交錯點)上,這樣的多邊形稱為格點多邊形.記格點多邊形內的格點數為![]() ,邊界上的格點數為
,邊界上的格點數為![]() ,則格點多邊形的面積可表示為
,則格點多邊形的面積可表示為![]() ,其中
,其中![]() ,
,![]() 為常數.
為常數.
(1)在下面的兩張方格紙中各有一個格點多邊形,依次為![]() 、正方形
、正方形![]() .認真數一數:
.認真數一數:![]() 內的格點數是_______,正方形
內的格點數是_______,正方形![]() 邊界上的格點數是_______;
邊界上的格點數是_______;
(2)利用(1)中的兩個格點多邊形確定![]() ,
,![]() 的值;
的值;
(3)現有一張方格紙共有200個格點,畫有一個格點多邊形,它的面積![]() ,若該格點多邊形外的格點數為
,若該格點多邊形外的格點數為![]() ,求
,求![]() 的值.
的值.


查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com