
【題目】在矩形ABCD中,AE⊥BD于點(diǎn)E,點(diǎn)P是邊AD上一點(diǎn).
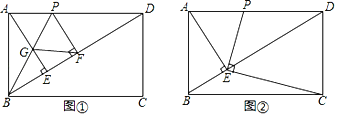
(1)若BP平分∠ABD,交AE于點(diǎn)G,PF⊥BD于點(diǎn)F,如圖①,證明四邊形AGFP是菱形;
(2)若PE⊥EC,如圖②,求證:AEAB=DEAP;
(3)在(2)的條件下,若AB=1,BC=2,求AP的長(zhǎng).
【答案】(1)見解析;(2)見解析;(3)![]()
【解析】
(1)想辦法證明AG=PF,AG∥PF,推出四邊形AGFP是平行四邊形,再證明PA=PF即可解決問題.
(2)證明△AEP∽△DEC,可得 ![]() ,由此即可解決問題.
,由此即可解決問題.
(3)利用(2)中結(jié)論.求出DE,AE即可.
(1)證明:如圖①中,
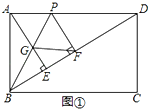
∵四邊形ABCD是矩形,
∴∠BAD=90°,
∵AE⊥BD,
∴∠AED=90°,
∴∠BAE+∠EAD=90°,∠EAD+∠ADE=90°,
∴∠BAE=∠ADE,
∵∠AGP=∠BAG+∠ABG,∠APD=∠ADE+∠PBD,∠ABG=∠PBD,
∴∠AGP=∠APG,
∴AP=AG,
∵PA⊥AB,PF⊥BD,BP平分∠ABD,
∴PA=PF,
∴PF=AG,
∵AE⊥BD,PF⊥BD,
∴PF∥AG,
∴四邊形AGFP是平行四邊形,
∵PA=PF,
∴四邊形AGFP是菱形.
(2)證明:如圖②中,
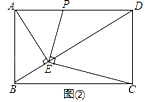
∵AE⊥BD,PE⊥EC,
∴∠AED=∠PEC=90°,
∴∠AEP=∠DEC,
∵∠EAD+∠ADE=90°,∠ADE+∠CDE=90°,
∴∠EAP=∠EDC,
∴△AEP∽△DEC,
∴![]() ,
,
∵AB=CD,
∴AEAB=DEAP;
(3)解:∵四邊形ABCD是矩形,
∴BC=AD=2,∠BAD=90°,
∴BD=![]() ,
,
∵AE⊥BD,
∴S△ABD=![]() BDAE=
BDAE=![]() ABAD,
ABAD,
∴AE=![]()
∴DE=![]() ,
,
∵AEAB=DEAP
∴AP=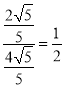 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小學(xué)生10分鐘應(yīng)用題系列答案
小學(xué)生10分鐘應(yīng)用題系列答案
| 年級(jí) | 高中課程 | 年級(jí) | 初中課程 |
| 高一 | 高一免費(fèi)課程推薦! | 初一 | 初一免費(fèi)課程推薦! |
| 高二 | 高二免費(fèi)課程推薦! | 初二 | 初二免費(fèi)課程推薦! |
| 高三 | 高三免費(fèi)課程推薦! | 初三 | 初三免費(fèi)課程推薦! |
科目:初中數(shù)學(xué) 來源: 題型:
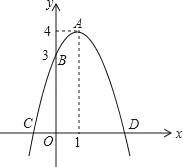
【題目】如圖,已知拋物線的頂點(diǎn)為A(1,4),拋物線與y軸交于點(diǎn)B(0,3),與x軸交于C、D兩點(diǎn).點(diǎn)P是x軸上的一個(gè)動(dòng)點(diǎn).
(1)求此拋物線的解析式;
(2)當(dāng)PA+PB的值最小時(shí),求點(diǎn)P的坐標(biāo).
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)![]() 交
交![]() 軸于點(diǎn)
軸于點(diǎn)![]() 、
、![]() ,交
,交![]() 軸于點(diǎn)
軸于點(diǎn)![]() ,在
,在![]() 軸上有一點(diǎn)
軸上有一點(diǎn)![]() ,連接
,連接![]() .
.

(1)求二次函數(shù)的表達(dá)式;
(2)若點(diǎn)![]() 為拋物線在
為拋物線在![]() 軸負(fù)半軸上方的一個(gè)動(dòng)點(diǎn),求
軸負(fù)半軸上方的一個(gè)動(dòng)點(diǎn),求![]() 面積的最大值;
面積的最大值;
(3)拋物線對(duì)稱軸上是否存在點(diǎn)![]() ,使
,使![]() 為等腰三角形,若存在,請(qǐng)直接寫出所有
為等腰三角形,若存在,請(qǐng)直接寫出所有![]() 點(diǎn)的坐標(biāo),若不存在請(qǐng)說明理由.
點(diǎn)的坐標(biāo),若不存在請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
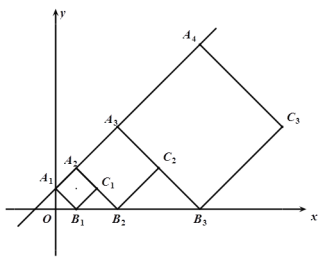
【題目】正方形![]() ,
, ![]() ,
,![]() ,…按如圖所示的方式放置,點(diǎn)
,…按如圖所示的方式放置,點(diǎn)![]() ,
,![]() ,
,![]() ,…和點(diǎn)
,…和點(diǎn)![]() ,
,![]() ,
,![]() ,…分別在直線
,…分別在直線![]() (
(![]() )和
)和![]() 軸上。已知
軸上。已知![]() ,點(diǎn)
,點(diǎn)![]() ,則
,則![]() 的坐標(biāo)是_____________
的坐標(biāo)是_____________
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
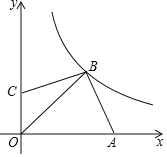
【題目】如圖所示平面直角坐標(biāo)系中,點(diǎn)A,C分別在x軸和y軸上,點(diǎn)B在第一象限,BC=BA,∠ABC=90°,反比例函數(shù)y=![]() .(x>0)的圖象經(jīng)過點(diǎn)B,若OB=2
.(x>0)的圖象經(jīng)過點(diǎn)B,若OB=2![]() ,則k的值為_____.
,則k的值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,已知直線y=![]() x+2與x軸、y軸分別交于點(diǎn)B,C,拋物線y=
x+2與x軸、y軸分別交于點(diǎn)B,C,拋物線y=![]() x2+bx+c過點(diǎn)B、C,且與x軸交于另一個(gè)點(diǎn)A.
x2+bx+c過點(diǎn)B、C,且與x軸交于另一個(gè)點(diǎn)A.
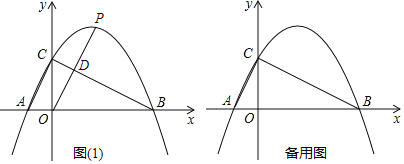
(1)求該拋物線的表達(dá)式;
(2)若點(diǎn)P是x軸上方拋物線上一點(diǎn),連接OP.
①若OP與線段BC交于點(diǎn)D,則當(dāng)D為OP中點(diǎn)時(shí),求出點(diǎn)P坐標(biāo).
②在拋物線上是否存在點(diǎn)P,使得∠POC=∠ACO若存在,求出點(diǎn)P坐標(biāo);若不存在,請(qǐng)說明理由.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在東西方向的海岸線l上有長(zhǎng)為300米的碼頭AB,在碼頭的最西端A處測(cè)得輪船M在它的北偏東45°方向上;同一時(shí)刻,在A點(diǎn)正東方向距離100米的C處測(cè)得輪船M在北偏東22°方向上.
(1)求輪船M到海岸線l的距離;(結(jié)果精確到0.01米)
(2)如果輪船M沿著南偏東30°的方向航行,那么該輪船能否行至碼頭AB靠岸?請(qǐng)說明理由.
(參考數(shù)據(jù):sin22°≈0.375,cos22°≈0.927,tan22°≈0.404,![]() ≈1.732.)
≈1.732.)

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,在平面直角坐標(biāo)系中,二次函數(shù)![]() 的圖像經(jīng)過點(diǎn)
的圖像經(jīng)過點(diǎn)![]() ,點(diǎn)
,點(diǎn)![]() ,與
,與![]() 軸交于點(diǎn)
軸交于點(diǎn)![]() ,
,
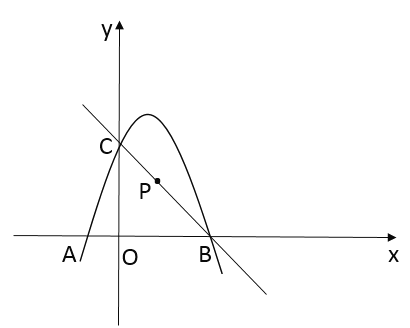
(1)求![]() 、
、![]() 的值:
的值:
(2)若點(diǎn)![]() 為直線
為直線![]() 上一點(diǎn),點(diǎn)
上一點(diǎn),點(diǎn)![]() 到直線
到直線![]() 、
、![]() 兩點(diǎn)的距離相等,將該拋物線向左(或向右)平移,得到一條新拋物線,并且新拋物線經(jīng)過點(diǎn)
兩點(diǎn)的距離相等,將該拋物線向左(或向右)平移,得到一條新拋物線,并且新拋物線經(jīng)過點(diǎn)![]() ,求新拋物線的頂點(diǎn)坐標(biāo).
,求新拋物線的頂點(diǎn)坐標(biāo).
查看答案和解析>>
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無(wú)主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com