
【題目】如圖,過拋物線y= ![]() x2﹣2x上一點A作x軸的平行線,交拋物線于另一點B,交y軸于點C,已知點A的橫坐標為﹣2.
x2﹣2x上一點A作x軸的平行線,交拋物線于另一點B,交y軸于點C,已知點A的橫坐標為﹣2.
(1)求拋物線的對稱軸和點B的坐標;
(2)在AB上任取一點P,連結OP,作點C關于直線OP的對稱點D;
①連結BD,求BD的最小值;
②當點D落在拋物線的對稱軸上,且在x軸上方時,求直線PD的函數表達式.
【答案】
(1)
解:由題意A(﹣2,5),對稱軸x=﹣ ![]() =4,
=4,
∵A、B關于對稱軸對稱,
∴B(10,5).
(2)
解:①如圖1中,
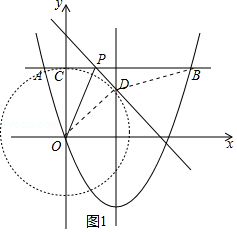
由題意點D在以O為圓心OC為半徑的圓上,
∴當O、D、B共線時,BD的最小值=OB﹣OD= ![]() ﹣5=5
﹣5=5 ![]() ﹣5.
﹣5.
②如圖中,
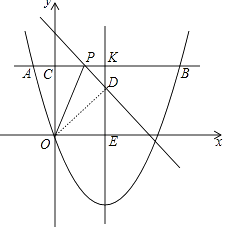
當點D在對稱軸上時,在Rt△ODE中,OD=OC=5,OE=4,
∴DE= ![]() =
= ![]() =3,
=3,
∴點D的坐標為(4,3).
設PC=PD=x,在Rt△PDK中,x2=(4﹣x)2+22,
∴x= ![]() ,
,
∴P( ![]() ,5),
,5),
∴直線PD的解析式為y=﹣ ![]() x+
x+ ![]() .
.
【解析】(1)思想確定點A的坐標,利用對稱軸公式求出對稱軸,再根據對稱性可得點B坐標;(2)①由題意點D在以O為圓心OC為半徑的圓上,推出當O、D、B共線時,BD的最小值=OB﹣OD;②當點D在對稱軸上時,在Rt△OD=OC=5,OE=4,可得DE= ![]() =
= ![]() =3,求出P、D的坐標即可解決問題;
=3,求出P、D的坐標即可解決問題;
【考點精析】通過靈活運用拋物線與坐標軸的交點,掌握一元二次方程的解是其對應的二次函數的圖像與x軸的交點坐標.因此一元二次方程中的b2-4ac,在二次函數中表示圖像與x軸是否有交點.當b2-4ac>0時,圖像與x軸有兩個交點;當b2-4ac=0時,圖像與x軸有一個交點;當b2-4ac<0時,圖像與x軸沒有交點.即可以解答此題.


科目:初中數學 來源: 題型:
【題目】綜合題。
(1)計算:(π﹣ ![]() )0+
)0+ ![]() +(﹣1)2013﹣
+(﹣1)2013﹣ ![]() tan60°;
tan60°;
(2)先化簡,再求值:(a+3)2+a(4﹣a),其中a為(1)中計算的結果.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】用若干個大小相同,棱長為1的小正方體搭成一個幾何體模型,其三視圖如圖所示,則搭成這個幾何體模型所用的小正方體的個數是( )

A. 4 B. 5 C. 6 D. 7
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,A點的初始位置位于數軸上表示1的點,現對A點做如下移動:第1次向左移動3個單位長度至B點,第2次從B點向右移動6個單位長度至C點,第3次從C點向左移動9個單位長度至D點,第4次從D點向右移動12個單位長度至E點,…,依此類推.這樣第_____次移動到的點到原點的距離為2018.
![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為創建大數據應用示范城市,我市某機構針對市民最關心的四類生活信息進行了民意調查(被調查者每人限選一項),下面是部分四類生活信息關注度統計圖表,請根據圖中提供的信息解答下列問題:
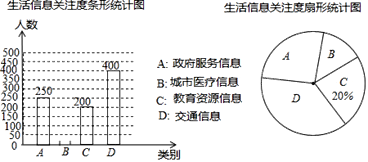
(1)本次參與調查的人數有______ 人;
(2)關注城市醫療信息的有______ 人,并補全條形統計圖;
(3)扇形統計圖中,D部分的圓心角是______度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小區準備新建50個停車位,用以解決小區停車難的問題.已知新建1個地上停車位和1個地下停車位共需0.6萬元;新建3個地上停車位和2個地下停車位共需1.3萬元.
(1)該小區新建1個地上停車位和1個地下停車位各需多少萬元?
(2)該小區的物業部門預計投資金額超過12萬元而不超過13萬元,那么共有幾種建造停車位的方案?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如果一元一次方程的解也是一元一次不等式組的解,則稱該一元一次方程為該不等式組的關聯方程.
例如:方程![]() 的解為
的解為![]() ,不等式組
,不等式組![]() 的解集為
的解集為![]() ,因為
,因為![]() ,所以,稱方程
,所以,稱方程![]() 為不等式組
為不等式組![]() 的關聯方程.
的關聯方程.
(1)在方程①![]() ,②
,②![]() ,③
,③![]() 中,不等式組
中,不等式組![]() 的關聯方程是 ;(填序號)
的關聯方程是 ;(填序號)
(2)若不等式組 的一個關聯方程的根是整數,則這個關聯方程可以是 ;(寫出一個即可)
的一個關聯方程的根是整數,則這個關聯方程可以是 ;(寫出一個即可)
(3)若方程![]() ,
,![]() 都是關于
都是關于![]() 的不等式組
的不等式組![]() 的關聯方程,求
的關聯方程,求![]() 的取值范圍.
的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,AB∥CD,EF與AB、CD分別相交于點E、F,EP⊥EF,與∠EFD的平分線FP相交于點P,且∠BEP=50°,則∠EPF=( )度. 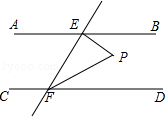
A.70
B.65
C.60
D.55
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com