
【題目】在平面直角坐標系中,![]() 為原點,拋物線
為原點,拋物線![]() 經過點
經過點![]() ,對稱軸為直線
,對稱軸為直線![]() ,點
,點![]() 關于直線
關于直線![]() 的對稱點為點
的對稱點為點![]() .過點
.過點![]() 作直線
作直線![]() 軸,交
軸,交![]() 軸于點
軸于點![]() .
.
(Ⅰ)求該拋物線的解析式及對稱軸;
(Ⅱ)點![]() 在
在![]() 軸上,當
軸上,當![]() 的值最小時,求點
的值最小時,求點![]() 的坐標;
的坐標;
(Ⅲ)拋物線上是否存在點![]() ,使得
,使得![]() ,若存在,求出點
,若存在,求出點![]() 的坐標;若不存在,請說明理由.
的坐標;若不存在,請說明理由.
【答案】(Ⅰ)拋物線的解析式為![]() ;拋物線的對稱軸為直線
;拋物線的對稱軸為直線![]() ;(Ⅱ)
;(Ⅱ)![]() 點坐標為
點坐標為![]() ;(Ⅲ)存在,
;(Ⅲ)存在,![]() 點坐標為
點坐標為![]() 或
或![]() ,理由見解析
,理由見解析
【解析】
(Ⅰ)將![]() 點代入二次函數的解析式,即可求出a,再根據對稱軸的公式即可求解.
點代入二次函數的解析式,即可求出a,再根據對稱軸的公式即可求解.
(Ⅱ)先求出B點胡坐標,要求![]() 胡最小值,只需找到B關于軸的對稱點
胡最小值,只需找到B關于軸的對稱點![]() ,則直線A
,則直線A![]() 與y軸的交點就是點P,根據待定系數法求出AB1的解析式,令y=0,即可求出P點的坐標.
與y軸的交點就是點P,根據待定系數法求出AB1的解析式,令y=0,即可求出P點的坐標.
(Ⅲ)設點Q的坐標,并求出△AOQ面積,從而得到△AOQ面積,根據Q點胡不同位置進行分類,用m及割補法求出面積方程,即可求解.
(Ⅰ)∵![]() 經過點
經過點![]() ,
,
∴![]() ,解得
,解得![]() ,
,
∴拋物線的解析式為![]() ,
,
∵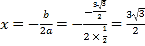 ,
,
∴拋物線的對稱軸為直線![]() .
.
(Ⅱ)∵點![]() ,對稱軸為
,對稱軸為![]() ,
,
∴點![]() 關于對稱軸的對稱點
關于對稱軸的對稱點![]() 點坐標為
點坐標為![]() .
.
作點![]() 關于軸的對稱點
關于軸的對稱點![]() ,得
,得![]() ,
,
設直線AB1的解析式為![]() ,
,
把點![]() ,點
,點![]() 代入得
代入得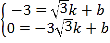 ,
,
解得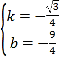 ,∴
,∴![]() .
.
∴直線![]() 與
與![]() 軸的交點即為
軸的交點即為![]() 點.
點.
令![]() 得
得![]() ,
,
∵![]() 點坐標為
點坐標為![]() .
.
(Ⅲ)∵![]() ,
,![]() 軸,∴
軸,∴![]() ,
,![]() ,
,
∴![]() ,
,
又∵![]() ,∴
,∴![]() .
.
設![]() 點坐標為
點坐標為![]() ,
,
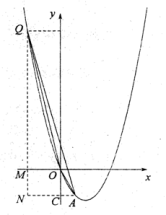
如圖情況一,作![]() ,交
,交![]() 延長線于點
延長線于點![]() ,
,
∵![]() ,
,
∴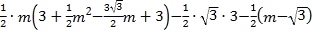
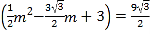 ,
,
化簡整理得![]() ,
,
解得![]() ,
,![]() .
.

如圖情況二,作![]() ,交
,交![]() 延長線于點
延長線于點![]() ,交
,交![]() 軸于點
軸于點![]() ,
,
∵![]() ,
,
∴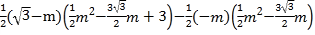
![]() ,
,
化簡整理得![]() ,
,
解得![]() ,
,![]() ,
,
∴![]() 點坐標為
點坐標為![]() 或
或![]() ,
,
∴拋物線上存在點![]() ,使得
,使得![]() .
.


科目:初中數學 來源: 題型:
【題目】在平行四邊形ABCD中,E為BC邊上的一點.連結AE.
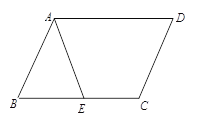
(1)若AB=AE, 求證:∠DAE=∠D;
(2)若點E為BC的中點,連接BD,交AE于F,求EF︰FA的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系![]() 中,對于點
中,對于點![]() 和點
和點![]() 給出如下定義:若
給出如下定義:若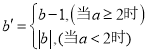 ,則稱點
,則稱點![]() 為點
為點![]() 的限變點.例如:點
的限變點.例如:點![]() 的限變點的坐標是
的限變點的坐標是![]() 點
點![]() 的限變點的坐標是
的限變點的坐標是![]() 點
點![]() 的限變點的坐標是
的限變點的坐標是![]() .
.
![]() ①點
①點![]() 的限變點的坐標是 ;
的限變點的坐標是 ;
②在點![]() 中有一個點是雙曲線
中有一個點是雙曲線![]() 上某一個點的限變點,這個點是(填“
上某一個點的限變點,這個點是(填“![]() ”或“
”或“![]() ”)
”)
![]() 若點
若點![]() 在關于
在關于![]() 的二次函數
的二次函數![]() 的圖象上,其限變點
的圖象上,其限變點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() 或
或![]() 其中
其中![]() .令
.令![]() ,直接寫出
,直接寫出![]() 的值.
的值.
![]() 若點
若點![]() 在函數
在函數![]() 的圖象上,其限變點
的圖象上,其限變點![]() 的縱坐標
的縱坐標![]() 的取值范圍是
的取值范圍是![]() ,直接寫出
,直接寫出![]() 的取值范圍;
的取值范圍;
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】周末上午小明和大強分別從家出發,相約一起去體育館打球,小明比大強先出發![]() ,大強出發
,大強出發![]() 后與小明相遇.小明的行進速度為
后與小明相遇.小明的行進速度為![]() ,設小明、大強兩人相距
,設小明、大強兩人相距![]() 與小明行進的時間
與小明行進的時間![]() 之間的函數關系如圖所示:
之間的函數關系如圖所示:
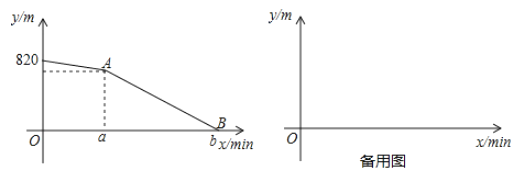
(1)填空:![]() ,小明和大強家相距
,小明和大強家相距 ![]() :
:
(2)求線段![]() 對應的函數表達式,并直接寫出自變量
對應的函數表達式,并直接寫出自變量![]() 的取值范圍;
的取值范圍;
(3)設大強離家的距離為![]() ,小明行進的時間
,小明行進的時間![]() ,求
,求![]() 與
與![]() 的函數關系式,并畫出函數的圖象.
的函數關系式,并畫出函數的圖象.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】八年級(1)班研究性學習小組為研究全校同學課外閱讀情況,在全校隨機邀請了部分同學參與問卷調查,統計同學們一個月閱讀課外書的數量,并繪制了如下的統計圖1和圖2,請根據圖中相關信息,解決下列問題:

(Ⅰ)圖1中![]() 的值為____________,共有____________名同學參與問卷調查;
的值為____________,共有____________名同學參與問卷調查;
(Ⅱ)求統計的這組數據的平均數、眾數和中位數;
(Ⅲ)全校共有學生1500人,根據樣本數據,估計該校學生一個月閱讀2本課外書的人數約為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
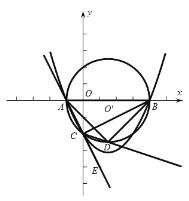
【題目】已知:二次函數![]() 的圖象與
的圖象與![]() 軸交于
軸交于![]() 兩點,其中點
兩點,其中點![]() ,與
,與![]() 軸負半軸交于點
軸負半軸交于點![]() ,起對稱軸是直線
,起對稱軸是直線![]() .
.
(1)求二次函數![]() 的解析式;
的解析式;
(2)圓![]() 經過點
經過點![]() 的外接圓,點
的外接圓,點![]() 是
是![]() 延長線上一點,
延長線上一點,![]() 的平分線交圓
的平分線交圓![]() 于點
于點![]() ,連接
,連接![]() 、
、![]() ,求
,求![]() 的面積;
的面積;
(3)在(2)的條件下,二次函數![]() 的圖象上是否存在點
的圖象上是否存在點![]() ,使得
,使得![]() ?如果存在,請求出所有符合條件的
?如果存在,請求出所有符合條件的![]() 點坐標;如果不存在,請說明理由.
點坐標;如果不存在,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知二次函數y ax2 2ax 3a2 3(其中x是自變量),當x 2時,y隨x的增大而增大,且3 x 0時,y的最大值為9,則a的值為( ).
A.1或![]() B.
B.![]() 或
或![]() C.
C.![]() D.1
D.1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直徑![]() 把圓
把圓![]() 分為兩個半圓,一個半圓弧上有一定點
分為兩個半圓,一個半圓弧上有一定點![]() ,另一半圓弧上有一動點
,另一半圓弧上有一動點![]() .過
.過![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
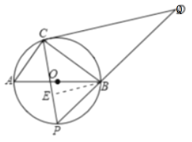
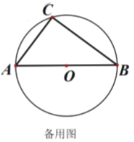
(1)求證:![]()
(2)若![]() ,
,![]()
①當點![]() 運動到半圓弧
運動到半圓弧![]() 中點時,求
中點時,求![]() 邊
邊![]() 上的高;
上的高;
②當點![]() 運動到什么位置時,
運動到什么位置時,![]() 的面積最大?并求這個最大面積
的面積最大?并求這個最大面積![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】黃岡市某高新企業制定工齡工資標準時充分考慮員工對企業發展的貢獻,同時提高員工的積極性、控制員工的流動率,對具有中職以上學歷員工制定如下的工齡工資方案.
Ⅰ.工齡工資分為社會工齡工資和企業工齡工資;
Ⅱ.社會工齡=參加本企業工作時年齡-18,
企業工齡=現年年齡-參加本企業工作時年齡.
Ⅲ.當年工作時間計入當年工齡
Ⅳ.社會工齡工資y1(元/月)與社會工齡x(年)之間的函數關系式如①圖所示,企業工齡工資y2(元/月)與企業工齡x(年)之間的函數關系如圖②所示.
請解決以下問題
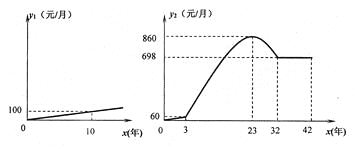
(1)求出y1、y2與工齡x之間的函數關系式;
(2)現年28歲的高級技工小張從18歲起一直在深圳實行同樣工齡工資制度的外地某企業工作,為了方便照顧老人與小孩,今年小張回鄉應聘到該企業,試計算第一年工齡工資每月下降多少元?
(3)已經在該企業工作超過3年的李工程師今年48歲,試求出他的工資最高每月多少元?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com