
【題目】已知直線![]() .
.
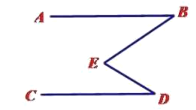
(1)如下圖,點![]() 在直線
在直線![]() 的左側,請寫出
的左側,請寫出![]() ,
,![]() ,
,![]() 之間的數量關系,并說明理由:
之間的數量關系,并說明理由:
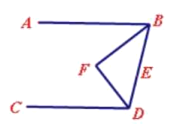
(2)如下圖,當點![]() 在線段
在線段![]() 上時,
上時,![]() 分別平分
分別平分![]() ,
,![]() ,此時
,此時![]() 的度數為_________°
的度數為_________°
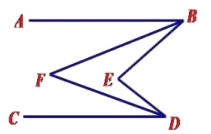
(3)如下圖,當點![]() 在直線
在直線![]() 的左側時,
的左側時,![]() 分別平分
分別平分![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 的數量關系 ;
的數量關系 ;
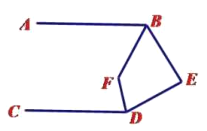
(4)如下圖,當點![]() 在直線
在直線![]() 的右側時,
的右側時,![]() 分別平分
分別平分![]() ,
,![]() ,請直接寫出
,請直接寫出![]() 和
和![]() 的數量關系 ;
的數量關系 ;
【答案】(1)∠ABE+∠CDE=∠BED,理由見解析;(2)90;(3)∠BFD=![]() ∠BED;(4)2∠BFD+∠BED=360°
∠BED;(4)2∠BFD+∠BED=360°
【解析】
(1)首先作EF∥AB,根據直線AB∥CD,可得EF∥CD,所以∠ABE=∠1,∠CDE=∠2,據此推得∠ABE+∠CDE=∠BED即可.
(2)作GF∥AB,根據∠ABD+∠CDB=180°,![]() 分別平分
分別平分![]() ,
,![]() ,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=
,得到∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() (∠ABD+∠CDB)=90°;
(∠ABD+∠CDB)=90°;
(3)首先根據BF,DF分別平分∠ABE,∠CDE,推得∠ABF+∠CDF=![]() (∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,據此推得∠BFD=
(∠ABE+∠CDE);然后由(1),可得∠BFD=∠ABF+∠CDF,∠BED=∠ABE+∠CDE,據此推得∠BFD=![]() ∠BED.
∠BED.
(4)首先過點E作EG∥CD,再根據AB∥CD,EG∥CD,推得AB∥CD∥EG,所以∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,據此推得∠ABE+∠CDE+∠BED=360°;然后根據∠BFD=∠ABF+∠CDF,以及BF,DF分別平分∠ABE,∠CDE,推得2∠BFD+∠BED=360°即可.
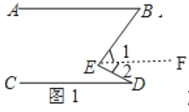
(1)∠ABE+∠CDE=∠BED.
理由:如圖1,作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠ABE=∠1,∠CDE=∠2,
∴∠ABE+∠CDE=∠1+∠2=∠BED,
即∠ABE+∠CDE=∠BED.
故答案為:∠ABE+∠CDE=∠BED;
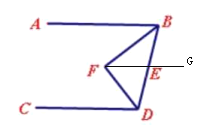
(2)如圖,作GF∥AB,
∴AB∥GF∥CD
∴∠ABD+∠CDB=180°,∠BFG=∠ABF,∠DFG=∠CDF
∵![]() 分別平分
分別平分![]() ,
,![]() ,
,
∴∠BFD=∠BFG+∠DFG=∠ABF+∠CDF=![]() ∠ABD +
∠ABD +![]() ∠CDB =
∠CDB =![]() (∠ABD+∠CDB)=90°,
(∠ABD+∠CDB)=90°,
故答案為:90;
(3)∠BFD=![]() ∠BED.
∠BED.
理由:如圖
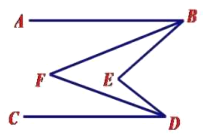
∵BF,DF分別平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠ABF+∠CDF=![]() ∠ABE+
∠ABE+![]() ∠CDE=
∠CDE=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
由(1)可得∠BFD=∠ABF+∠CDF=![]() (∠ABE+∠CDE)
(∠ABE+∠CDE)
又∠BED=∠ABE+∠CDE,
∴∠BFD=![]() ∠BED.
∠BED.
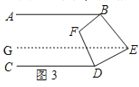
(4)2∠BFD+∠BED=360°.
理由:如圖3,過點E作EG∥CD,
∵AB∥CD,EG∥CD,
∴AB∥CD∥EG,
∴∠ABE+∠BEG=180°,∠CDE+∠DEG=180°,
∴∠ABE+∠CDE+∠BED=360°,
由(1)知,∠BFD=∠ABF+∠CDF,
又∵BF,DF分別平分∠ABE,∠CDE,
∴∠ABF=![]() ∠ABE,∠CDF=
∠ABE,∠CDF=![]() ∠CDE,
∠CDE,
∴∠BFD=![]() (∠ABE+∠CDE),
(∠ABE+∠CDE),
∴2∠BFD+∠BED=360°.
故答案為:2∠BFD+∠BED=360°.


科目:初中數學 來源: 題型:
【題目】如圖,直角三角形紙片的兩直角邊長分別為6、8,按如圖那樣折疊,使點A與點B重合,折痕為DE,則S△BCE:S△BDE等于( )

A.2:5 B.14:25 C.16:25 D.4:21
查看答案和解析>>
科目:初中數學 來源: 題型:
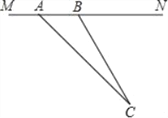
【題目】“為了安全,請勿超速”,如圖所示是一條已經建成并通車的公路,且該公路的某直線路段MN上限速17m/s,為了檢測來往車輛是否超速,交警在MN旁設立了觀測點C.若某次從觀測點C測得一汽車從點A到達點B行駛了5秒鐘,已知∠CAN=45°,∠CBN=60°,BC=200m.
(1)求觀測點C到公路MN的距離;
(2)請你判斷該汽車是否超速?(參考數據:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在平面直角坐標系xOy中,已知A(2t,0),B(0,-2t),C(2t,4t)三點,其中t>0,函數![]() 的圖象分別與線段BC,AC交于點P,Q.若S△PAB-S△PQB=t,則t的值為__.
的圖象分別與線段BC,AC交于點P,Q.若S△PAB-S△PQB=t,則t的值為__.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】小明家飲水機中原有水的溫度為20℃,通電開機后,飲水機自動開始加熱[此過程中水溫y(℃)與開機時間x(分)滿足一次函數關系],當加熱到100℃時自動停止加熱,隨后水溫開始下降[此過程中水溫y(℃)與開機時間x(分)成反比例關系],當水溫降至20℃時,飲水機又自動開始加熱…,重復上述程序(如圖所示),根據圖中提供的信息,解答下列問題:
(1)當0≤x≤8時,求水溫y(℃)與開機時間x(分)的函數關系式;
(2)求圖中t的值;
(3)若小明在通電開機后即外出散步,請你預測小明散步45分鐘回到家時,飲水機內的溫度約為多少℃?

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列各式中:
①由3x=﹣4系數化為1得x=﹣![]() ;
;
②由5=2﹣x移項得x=5﹣2;
③由![]() 去分母得2(2x﹣1)=1+3(x﹣3);
去分母得2(2x﹣1)=1+3(x﹣3);
④由2(2x﹣1)﹣3(x﹣3)=1去括號得4x﹣2﹣3x﹣9=1.
其中正確的個數有( )
A. 0個 B. 1個 C. 3個 D. 4個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖所示,AB∥DE,AC∥DF,AC=DF下列條件中,不能判斷△ABC≌△DEF的是( )

A. AB=DE B. ∠B=∠E C. EF=BC D. EF∥BC
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】現代互聯網技術的廣泛應用,催生了快遞行業的高速發展.小明計劃給朋友快遞一部分物品,經了解有甲、乙兩家快遞公司比較合適.甲公司表示:快遞物品不超過1千克的,按每千克22元收費;超過1千克,超過的部分按每千克15元收費.乙公司表示:按每千克16元收費,另加包裝費3元.設小明快遞物品x千克.
(1)請分別寫出甲、乙兩家快遞公司快遞該物品的費用y(元)與x(千克)之間的函數關系式;
(2)小明選擇哪家快遞公司更省錢?
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com