
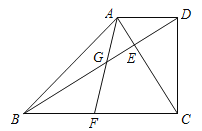
【題目】已知:如圖,在梯形ABCD中,AD//BC,∠BCD=90,對角線AC、BD相交于點E,且AC⊥BD.
(1)求證:![]() ;
;
(2)點F是邊BC上一點,聯結AF,與BD相交于點G.如果∠BAF =∠DBF,求證:![]() .
.
【答案】(1)參見解析;(2)參見解析.
【解析】
試題分析:(1)利用已知條件和同角的余角相等得出∠ACD=∠CBD.再根據∠ADC=∠BCD=90.因為兩角對應相等,兩個三角形相似,所以△ACD∽△DBC.相似三角形對應邊成比例,所以![]() ,從而得出結論;(2)利用平行線的性質和等量代換得出∠ADB=∠BAF.從而判定△ABG∽△DBA.得出
,從而得出結論;(2)利用平行線的性質和等量代換得出∠ADB=∠BAF.從而判定△ABG∽△DBA.得出![]() ,即
,即![]() ,又因為
,又因為![]() ,得出
,得出![]() ,代入前面的式子中即可得出結論.
,代入前面的式子中即可得出結論.
試題解析:(1)∵AD//BC,∠BCD=90,∴∠ADC=∠BCD=90.又∵AC⊥BD,∴∠ACD+∠ACB=∠CBD+∠ACB=90.∴∠ACD=∠CBD.∴△ACD∽△DBC.∴![]() ,即
,即![]() ;(2)∵AD//BC,∴∠ADB=∠DBF.∵∠BAF=∠DBF,∴∠ADB=∠BAF.∵∠ABG=∠DBA,∴△ABG∽△DBA.∴
;(2)∵AD//BC,∴∠ADB=∠DBF.∵∠BAF=∠DBF,∴∠ADB=∠BAF.∵∠ABG=∠DBA,∴△ABG∽△DBA.∴![]() .兩邊同時平方得:
.兩邊同時平方得:![]() .又由于△ABG∽△DBA,∴
.又由于△ABG∽△DBA,∴![]() .
.
∴![]() .∴
.∴![]() .
.


科目:初中數學 來源: 題型:
【題目】工人師傅用一塊長為10dm,寬為6dm的矩形鐵皮制作一個無蓋的長方體容器,需要將四角各裁掉一個正方形.(厚度不計)

(1)在圖中畫出裁剪示意圖,用實線表示裁剪線,虛線表示折痕;并求長方體底面面積為12dm2時,裁掉的正方形邊長多大?
(2)若要求制作的長方體的底面長不大于底面寬的五倍,并將容器進行防銹處理,側面每平方分米的費用為0.5元,底面每平方分米的費用為2元,裁掉的正方形邊長多大時,總費用最低,最低為多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,![]() ,
,![]() 是直線
是直線![]() 與坐標軸的交點,直線
與坐標軸的交點,直線![]() 過點
過點![]() ,與
,與![]() 軸交于點
軸交于點![]() .
.
(1)求![]() ,
,![]() ,
,![]() 三點的坐標.
三點的坐標.
(2)當點![]() 是
是![]() 的中點時,在
的中點時,在![]() 軸上找一點
軸上找一點![]() ,使
,使![]() 的和最小,畫出點
的和最小,畫出點![]() 的位置,并求
的位置,并求![]() 點的坐標.
點的坐標.
(3)若點![]() 是折線
是折線![]() 上一動點,是否存在點
上一動點,是否存在點![]() ,使
,使![]() 為直角三角形,若存在,直接寫出
為直角三角形,若存在,直接寫出![]() 點的坐標;若不存在,請說明理由.
點的坐標;若不存在,請說明理由.
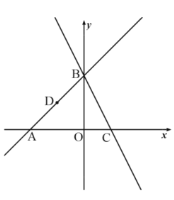
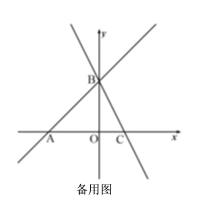

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法“①凡正方形都相似;②凡等腰三角形都相似;③凡等腰直角三角形都相似;④直角三角形斜邊上的中線與斜邊的比為![]() ;⑤兩個相似多邊形的面積比為
;⑤兩個相似多邊形的面積比為![]() ,則周長的比為
,則周長的比為![]() .”中,正確的個數有( )個
.”中,正確的個數有( )個
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,已知正方形![]() 的邊長為
的邊長為![]() ,有一動點
,有一動點![]() 以
以![]() 的速度沿
的速度沿![]() 的路徑運動,設
的路徑運動,設![]() 點運動的時間為
點運動的時間為![]() ,
,![]() 的面積為
的面積為![]()
![]() .
.
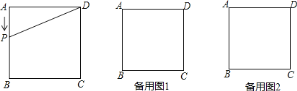
![]() 當
當![]() 是等腰直角三角形時,直接寫出
是等腰直角三角形時,直接寫出![]() 的值.答:
的值.答:![]() ________;
________;
![]() 求
求![]() 與
與![]() 的函數關系式并寫出自變量
的函數關系式并寫出自變量![]() 的取值范圍;
的取值范圍;
![]() 當
當![]() 為何值時,
為何值時,![]() 的面積為
的面積為![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
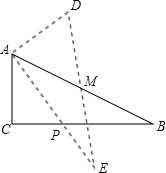
【題目】如圖,在△ABC中,∠C=90°,AB=10,cosB=![]() ,點M是AB邊的中點,將△ABC繞著點M旋轉,使點C與點A重合,點A與點D重合,點B與點E重合,得到△DEA,且AE交CB于點P,那么線段CP的長是__________.
,點M是AB邊的中點,將△ABC繞著點M旋轉,使點C與點A重合,點A與點D重合,點B與點E重合,得到△DEA,且AE交CB于點P,那么線段CP的長是__________.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀理解:
材料![]() .若一元二次方程
.若一元二次方程 ![]() 的兩根為
的兩根為 ![]() ,
,![]() ,則
,則![]() ,
,![]() .
.
材料![]() .已知實數
.已知實數 ![]() ,
,![]() 滿足
滿足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求![]() 的值.
的值.
解:由題知 ![]() ,
,![]() 是方程
是方程 ![]() 的兩個不相等的實數根,
的兩個不相等的實數根,
根據材料 ![]() 得
得 ![]() ,
,![]() ,
,
∴![]() .
.
解決問題:
(1)一元二次方程 ![]() 的兩根為
的兩根為 ![]() ,
,![]() ,則
,則 ![]() ,
,![]() .
.
(2)已知實數 ![]() ,
,![]() 滿足
滿足 ![]() ,
,![]() ,且
,且![]() ,求
,求
![]() 的值.
的值.
(3)已知實數 ![]() ,
,![]() 滿足
滿足 ![]() ,
,![]() ,且
,且 ![]() ,求
,求 ![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,一艘漁船正以60海里/小時的速度向正東方向航行,在A處測得島礁P在東北方向上,繼續航行1.5小時后到達B處此時測得島礁P在北偏東30°方向,同時測得島礁P正東方向上的避風港M在北偏東60°方向。為了在臺風到來之前用最短時間到達M處,漁船立刻加速以75海里/小時的速度繼續航行多少小時即可到達? (結果保留根號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,△ABC的三個頂點坐標都在格點上,且△A1B1C1與△ABC關于原點O成中心對稱,C點坐標為(-2,1)。
(1)請直接寫出A1的坐標 ;并畫出△A1B1C1.
(2)P(a,b)是△ABC的AC邊上一點,將△ABC平移后點P的對稱點P'(a+2,b﹣6),請畫出平移后的△A2B2C2.
(3)若△A1B1C1和△A2B2C2關于某一點成中心對稱,則對稱中心的坐標為 .

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com