
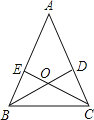
【題目】如圖,△ABC中,AB=AC,兩條角平分線BD、CE相交于點O.
(1)證明:△ABD≌△ACE;(2)證明:OB=OC.
【答案】見解析
【解析】試題分析:(1)、根據等腰三角形的性質和角平分線的性質得出∠ABD=∠ACE,然后結合∠A=∠A,AB=AC,根據ASA來判定兩個三角形全等;(2)、根據等腰三角形和角平分線的性質得出∠DBC=∠ECB,從而得到△OBC為等腰三角形,從而得出答案.
試題解析:(1)證明:∵AB=AC,
∴∠ABC=∠ACB
∵兩條角平分線BD、CE相交于點O
∴∠ABD=∠ACE,
在△ABD和△ACE中,
∠ABD=∠ACE,AB=AC,∠A=∠A,
△ABD≌△ACE.
(2)證明:∵AB=AC,
∴∠ABC=∠ACB,
∵兩條角平分線BD、CE相交于點O
∴∠DBC=∠ECB
∴OB=OC


 小學課堂作業系列答案
小學課堂作業系列答案 金博士一點全通系列答案
金博士一點全通系列答案科目:初中數學 來源: 題型:
【題目】(10分)如圖,一次函數![]() 與反比例函數
與反比例函數![]() 的圖象交于A(1,4),B(4,n)兩點.
的圖象交于A(1,4),B(4,n)兩點.

(1)求反比例函數的解析式;
(2)求一次函數的解析式;
(3)點P是x軸上的一動點,試確定點P并求出它的坐標,使PA+PB最小.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】操作題:公元初,中美洲瑪雅人使用的一種數字系統與其他計數方式都不相同,它采用二十進位制但只有3個符號,用點“”劃“”、卵形“![]() ”來表示我們所使用的自然數,如自然數1~19的表示見下表,另外在任何數的下方加一個卵形,就表示把這個數擴大到它的20倍,如表中20和100的表示.
”來表示我們所使用的自然數,如自然數1~19的表示見下表,另外在任何數的下方加一個卵形,就表示把這個數擴大到它的20倍,如表中20和100的表示.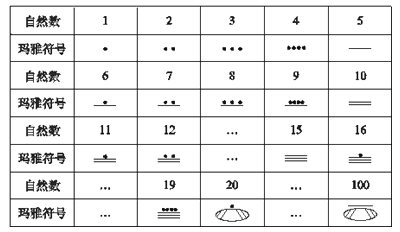
(1)瑪雅符號 ![]() 表示的自然數是 ;
表示的自然數是 ;
(2)請你在右邊的方框中畫出表示自然數280的瑪雅符號: .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,C為線段AE上一動點(不與點A,E重合),在AE同側分別作等邊△ABC和等邊△CDE,AD與BE交于點O,AD與BC交于點P,BE與CD交于點Q,連接PQ.以下五個結論:
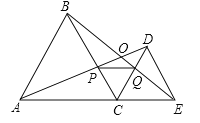
①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正確的結論的個數是( )
A. 2個 B. 3個 C. 4個 D. 5個
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】列方程解應用題:
為了豐富社會實踐活動,引導學生科學探究,學校組織七年級同學走進中國科技館,親近科學,感受科技魅力.來到科技館大廳,同學們就被大廳里會“跳舞”的“小球矩陣”吸引住了(如圖1).白色小球全部由計算機精準控制,每一只小球可以“懸浮”在大廳上空的不同位置,演繹著曲線、曲面、平面、文字和三維圖案等各種動態造型.
已知每個小球分別由獨立的電機控制.圖2,圖3分別是9個小球可構成的兩個造型,在每個造型中,相鄰小球的高度差均為a.為了使小球從造型一(如圖2)變到造型二(如圖3),控制電機使造型一中的②,③,④,⑥,⑦,⑧號小球同時運動,②,③,④號小球向下運動,運動速度均為3米/秒;⑥,⑦,⑧號小球向上運動,運動速度均為2米/秒,當每個小球到達造型二的相應位置時就停止運動.已知⑦號小球比②號小球晚![]() 秒到達相應位置,問②號小球運動了多少米?
秒到達相應位置,問②號小球運動了多少米?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,拋物線y=![]() (其中m>1)與其對稱軸l相交于點P,與y軸相交于點A(0,m).點A關于直線l的對稱點為B,作BC⊥x軸于點C,連接PC、PB,與拋物線、x軸分別相交于點D、E,連接DE.將△PBC沿直線PB翻折,得到△PBC′.
(其中m>1)與其對稱軸l相交于點P,與y軸相交于點A(0,m).點A關于直線l的對稱點為B,作BC⊥x軸于點C,連接PC、PB,與拋物線、x軸分別相交于點D、E,連接DE.將△PBC沿直線PB翻折,得到△PBC′.
(1)該拋物線的解析式為 ; (用含m的式子表示);
(2)探究線段DE、BC的關系,并證明你的結論;
(3)直接寫出C′點的坐標(用含m的式子表示).

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com