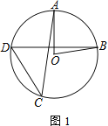
【題目】如圖，在⊙O中，半徑OA與弦BD垂直，點C在⊙O上，∠AOB＝80°
(1) 若點C在優弧BD上，求∠ACD的大小
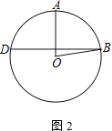
(2) 若點C在劣弧BD上，直接寫出∠ACD的大小
科目：初中數學 來源： 題型：
【題目】如圖，在平面直角坐標系中，已知矩形
的三個頂點
、
、
.拋物線的解析式為
.
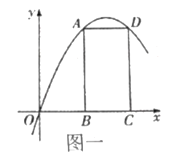
（1）如圖一，若拋物線經過
，
兩點，直接寫出點的坐標 ；拋物線的對稱軸為直線 ；
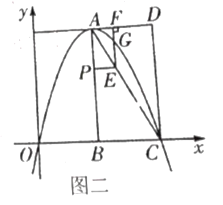
（2）如圖二：若拋物線經過、
兩點，
①求拋物線的表達式.
②若點
為線段
上一動點，過點作
交
于點
，過點作
于點
交拋物線于點
.當線段
最長時，求點的坐標；
（3）若
，且拋物線與矩形沒有公共點，直接寫出
的取值范圍.
查看答案和解析>>
科目：初中數學 來源： 題型：
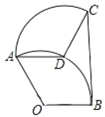
【題目】如圖，將半徑為1，圓心角為120°的扇形OAB繞點A逆時針旋轉一個角度，使點O的對應點D落在弧AB上，點B的對應點為C，連接BC，則圖中CD、BC和弧BD圍成的封閉圖形面積是（ ）
A. 
B. 
C. 
D. 
查看答案和解析>>
科目：初中數學 來源： 題型：
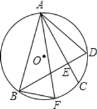
【題目】如圖，半徑為R的⊙O的弦AC＝BD，AC、BD交于E，F為
上一點，連AF、BF、AB、AD，下列結論：①AE＝BE；②若AC⊥BD，則AD＝
R；③在②的條件下，若
，AB＝，則BF+CE＝1．其中正確的是（ ）
A.①②B.①③C.②③D.①②③
查看答案和解析>>
科目：初中數學 來源： 題型：
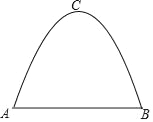
【題目】一條單車道的拋物線形隧道如圖所示．隧道中公路的寬度AB＝8m，隧道的最高點C到公路的距離為6m．
（1）建立適當的平面直角坐標系，求拋物線的表達式；
（2）現有一輛貨車的高度是4.4m，貨車的寬度是2m，為了保證安全，車頂距離隧道頂部至少0.5m，通過計算說明這輛貨車能否安全通過這條隧道．
查看答案和解析>>
科目：初中數學 來源： 題型：
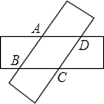
【題目】如圖，剪兩張對邊平行且寬度相同的紙條隨意交叉疊放在一起，轉動其中一張，重合部分構成一個四邊形，則下列結論中不一定成立的是（ ）
A. ∠ABC＝∠ADC，∠BAD＝∠BCDB. AB＝BC
C. AB＝CD，AD＝BCD. ∠DAB+∠BCD＝180°
查看答案和解析>>
科目：初中數學 來源： 題型：
【題目】如圖，認真觀察下面這些算式，并結合你發現的規律，完成下列問題：
算式①
，
算式②
，
算式③
，
算式④
，
…
（1）請寫出：算式③______；算式④______；
（2）上述算式的規律可以用文字概括為：“兩個連續奇數的平方差能被8整除”，如果設兩個連續奇數分別為
和
（
為整數），請說明這個規律是成立的；
（3）你認為“兩個連續偶數的平方差能被8整除”這個說法是否也成立呢？請說明理由.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com
