
【題目】如圖,拋物線y=ax2+bx+2與x軸交于點A(1,0)和B(4,0).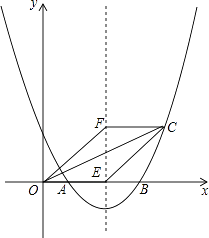
(1)求拋物線的解析式;
(2)若拋物線的對稱軸交x軸于點E,點F是位于x軸上方對稱軸上一點,FC∥x軸,與對稱軸右側的拋物線交于點C,且四邊形OECF是平行四邊形,求點C的坐標;
(3)在(2)的條件下,拋物線的對稱軸上是否存在點P,使△OCP是直角三角形?若存在,求出點P的坐標;若不存在,請說明理由.
【答案】
(1)
解:把點A(1,0)和B(4,0)代入y=ax2+bx+2得,
![]() ,
,
解得 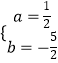 ,
,
所以,拋物線的解析式為y= ![]() x2﹣
x2﹣ ![]() x+2
x+2
(2)
解:方法一:
拋物線的對稱軸為直線x= ![]() ,
,
∵四邊形OECF是平行四邊形,
∴點C的橫坐標是 ![]() ×2=5,
×2=5,
∵點C在拋物線上,
∴y= ![]() ×52﹣
×52﹣ ![]() ×5+2=2,
×5+2=2,
∴點C的坐標為(5,2)
方法二:
∵FC∥x軸,∴當FC=OE時,四邊形OECF是平行四邊形.
設C(t, ![]() ),
),
∴F( ![]() ,
, ![]() +2),
+2),
∴t﹣ ![]() =
= ![]() ,
,
∴t=5,C(5,2)
(3)
解:方法一:
設OC與EF的交點為D,
∵點C的坐標為(5,2),
∴點D的坐標為( ![]() ,1),
,1),
①點O是直角頂點時,易得△OED∽△PEO,
∴ ![]() ,
,
即 ![]() =
= ![]() ,
,
解得PE= ![]() ,
,
所以,點P的坐標為( ![]() ,﹣
,﹣ ![]() );
);
②點C是直角頂點時,同理求出PF= ![]() ,
,
所以,PE= ![]() +2=
+2= ![]() ,
,
所以,點P的坐標為( ![]() ,
, ![]() );
);
③點P是直角頂點時,由勾股定理得,OC= ![]() =
= ![]() ,
,
∵PD是OC邊上的中線,
∴PD= ![]() OC=
OC= ![]() ,
,
若點P在OC上方,則PE=PD+DE= ![]() +1,
+1,
此時,點P的坐標為( ![]() ,
, ![]() ),
),
若點P在OC的下方,則PE=PD﹣DE= ![]() ﹣1,
﹣1,
此時,點P的坐標為( ![]() ,
, ![]() ),
),
綜上所述,拋物線的對稱軸上存在點P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形
),使△OCP是直角三角形
方法二:
∵點P在拋物線的對稱軸上,設P( ![]() ,t),O(0,0),C(5,2),
,t),O(0,0),C(5,2),
∵△OCP是直角三角形,∴OC⊥OP,OC⊥PC,OP⊥PC,
①OC⊥OP,∴KOC×KOP=﹣1,∴ ![]() ,
,
∴t=﹣ ![]() ,∴P(
,∴P( ![]() ,﹣
,﹣ ![]() ),
),
②OC⊥PC,∴KOC×KPC=﹣1,∴ ![]() =﹣1,
=﹣1,
∴t= ![]() ,P(
,P( ![]() ,
, ![]() ),
),
③OP⊥PC,∴KOP×KPC=﹣1,∴ ![]() ,
,
∴4t2﹣8t﹣25=0,∴t= ![]() 或
或 ![]() ,
,
點P的坐標為( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),
),
綜上所述,拋物線的對稱軸上存在點P( ![]() ,﹣
,﹣ ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() )或(
)或( ![]() ,
, ![]() ),使△OCP是直角三角形.
),使△OCP是直角三角形.
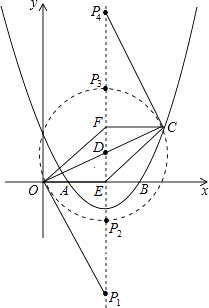
【解析】方法一:(1)把點A、B的坐標代入函數解析式,解方程組求出a、b的值,即可得解;(2)根據拋物線解析式求出對稱軸,再根據平行四邊形的對角線互相平分求出點C的橫坐標,然后代入函數解析式計算求出縱坐標,即可得解;(3)設AC、EF的交點為D,根據點C的坐標寫出點D的坐標,然后分①點O是直角頂點時,求出△OED和△PEO相似,根據相似三角形對應邊成比例求出PE,然后寫出點P的坐標即可;②點C是直角頂點時,同理求出PF,再求出PE,然后寫出點P的坐標即可;③點P是直角頂點時,利用勾股定理列式求出OC,然后根據直角三角形斜邊上的中線等于斜邊的一半可得PD= ![]() OC,再分點P在OC的上方與下方兩種情況寫出點P的坐標即可.
OC,再分點P在OC的上方與下方兩種情況寫出點P的坐標即可.
方法二:(1)略.(2)因為四邊形OECF是平行四邊形,且FC∥x軸,列出F,C的參數坐標,利用FC=OE,可求出C點坐標.(3)列出點P的參數坐標,分別列出O,C兩點坐標,由于△OCP是直角三角形,所以分別討論三種垂直的位置關系,利用斜率垂直公式,可求出三種情況下點P的坐標.
【考點精析】關于本題考查的二次函數的性質,需要了解增減性:當a>0時,對稱軸左邊,y隨x增大而減小;對稱軸右邊,y隨x增大而增大;當a<0時,對稱軸左邊,y隨x增大而增大;對稱軸右邊,y隨x增大而減小才能得出正確答案.


科目:初中數學 來源: 題型:
【題目】某學校計劃購進A,B兩種樹木共100棵進行校園綠化升級,經市場調查:購買A種樹木2棵,B種樹木5棵,共需600元;購買A種樹木3棵,B種樹木1棵,共需380元.
![]() 求A種,B種樹木每棵各多少元?
求A種,B種樹木每棵各多少元?
![]() 因布局需要,購買A種樹木的數量不少于B種樹木數量的3倍
因布局需要,購買A種樹木的數量不少于B種樹木數量的3倍![]() 學校與中標公司簽訂的合同中規定:在市場價格不變的情況下
學校與中標公司簽訂的合同中規定:在市場價格不變的情況下![]() 不考慮其他因素
不考慮其他因素![]() ,實際付款總金額按市場價九折優惠,請設計一種購買樹木的方案,
,實際付款總金額按市場價九折優惠,請設計一種購買樹木的方案,
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在四邊形ABCD中,AB=AD,CB=CD,對角線AC,BD相交于點O,下列結論中:
①∠ABC=∠ADC;
②AC與BD相互平分;
③AC,BD分別平分四邊形ABCD的兩組對角;
④四邊形ABCD的面積S=![]() ACBD.
ACBD.
正確的是 (填寫所有正確結論的序號)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】武警戰士乘一沖鋒舟從![]() 地逆流而上,前往
地逆流而上,前往![]() 地營救受困群眾,途經
地營救受困群眾,途經![]() 地時,由所攜帶的救生艇將
地時,由所攜帶的救生艇將![]() 地受困群眾運回
地受困群眾運回![]() 地,沖鋒舟繼續前進,到
地,沖鋒舟繼續前進,到![]() 地接到群眾后立刻返回
地接到群眾后立刻返回![]() 地,途中曾與救生艇相遇.沖鋒舟和救生艇距
地,途中曾與救生艇相遇.沖鋒舟和救生艇距![]() 地的距離
地的距離![]() (千米)和沖鋒舟出發后所用時間
(千米)和沖鋒舟出發后所用時間![]() (分)之間的函數圖象如圖所示.假設營救群眾的時間忽略不計,水流速度和沖鋒舟在靜水中的速度不變.
(分)之間的函數圖象如圖所示.假設營救群眾的時間忽略不計,水流速度和沖鋒舟在靜水中的速度不變.

(1)請直接寫出沖鋒舟從![]() 地到
地到![]() 地所用的時間.
地所用的時間.
(2)求水流的速度.
(3)沖鋒舟將![]() 地群眾安全送到
地群眾安全送到![]() 地后,又立即去接應救生艇.已知救生艇與
地后,又立即去接應救生艇.已知救生艇與![]() 地的距離
地的距離![]() (千米)和沖鋒舟出發后所用時間
(千米)和沖鋒舟出發后所用時間![]() (分)之間的函數關系式為
(分)之間的函數關系式為![]() ,假設群眾上下船的時間不計,求沖鋒舟在距離
,假設群眾上下船的時間不計,求沖鋒舟在距離![]() 地多遠處與救生艇第二次相遇?
地多遠處與救生艇第二次相遇?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】2018年在中央“房子是用來住的,不是用來炒”的精神作用下,房子價格持續下跌.玲玲家買了一套新房準備裝修,若甲、乙兩個裝飾公司合作,需6周完成,共需裝修費為5.2萬元;若甲公司單獨做4周后,剩下的由乙公司來做,還需9周才能完成,共需裝修費為4.8萬元.玲玲的爸爸媽媽商量后決定只選一個公司單獨完成.
(1)如果從節約時間的角度考慮應選哪家公司?
(2)如果從節約開支的角度考慮應選哪家公司?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】甲騎自行車、乙騎摩托車沿相同路線由A地到B地,行駛過程中路程與時間的函數關系的圖象如圖. 根據圖象解決下列問題:
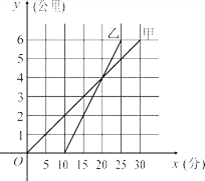
(1) 誰先出發?先出發多少時間?誰先到達終點?先到多少時間?
(2) 分別求出甲、乙兩人的行駛速度;
(3) 在什么時間段內,兩人均行駛在途中(不包括起點和終點)?在這一時間段內,請你根據下列情形,分別列出關于行駛時間x的方程或不等式(不化簡,也不求解):① 甲在乙的前面;② 甲與乙相遇;③ 甲在乙后面.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】在某地,人們發現某種蟋蟀1min,所叫次數x與當地溫度T之間的關系或為T=ax+b,下面是蟋蟀所叫次數與溫度變化情況對照表:
蟋蟀叫的次數(x) | … | 84 | 98 | 119 | … |
溫度(℃)T | … | 15 | 17 | 20 | … |
①根據表中的數據確定a、b的值.
②如果蟋蟀1min叫63次,那么該地當時的溫度約為多少攝氏度?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】為鼓勵居民節約用電,電力公司規定如下電費計算方法:每月用電不超過100度,按每度0.6元計費;每月用電超過100度,超過部分按每度1元計費.
(1)若某用戶某年1月交電費88元,那么該用戶1月份用電多少度?
(2)若某用戶某年2月份平均每度電費0.75元,那么該用戶2月份用電多少度?應交電費多少元?
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB>AC,點D、E分別是邊AB、AC的中點,點F在BC邊上,連接DE、DF、EF,則添加下列哪一個條件后,仍無法判斷△FCE與△EDF全等( )

A. ∠A=∠DFE B. BF=CF C. DF∥AC D. ∠C=∠EDF
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com