
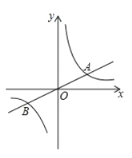
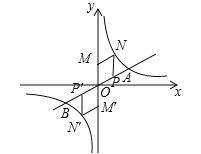
【題目】如圖,已知直線![]() 與雙曲線
與雙曲線![]() 交于 A、B 兩點,且點A的橫坐標
交于 A、B 兩點,且點A的橫坐標![]() .
.
(1)求 k 的值;
(2)若雙曲線 ![]() 上點 C 的縱坐標為 3,求△AOC 的面積;
上點 C 的縱坐標為 3,求△AOC 的面積;
(3)在 y 軸上有一點 M,在直線 AB 上有一點 P,在雙曲線![]() 上有一點 N,若四邊形OPNM 是有一組對角為 60°的菱形,請寫出所有滿足條件的點 P 的坐標.
上有一點 N,若四邊形OPNM 是有一組對角為 60°的菱形,請寫出所有滿足條件的點 P 的坐標.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)P點坐標為
;(3)P點坐標為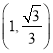 或
或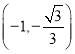 .
.
【解析】
(1)把點A的橫坐標![]() 代入
代入![]() 中,求出A點坐標,再把A點坐標代入
中,求出A點坐標,再把A點坐標代入![]() 中求出k的值即可;
中求出k的值即可;
(2)先求出AC解析式,然后求出D點坐標,從而求出△AOC的面積;
(3)設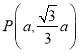 ,則
,則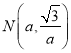 ,根據菱形的鄰邊相等,可得關于a的方程,解出a即可.
,根據菱形的鄰邊相等,可得關于a的方程,解出a即可.
解:(1)把點A的橫坐標![]() 代入
代入![]() 中,
中,
得:![]() ,
,
∴A點坐標為![]() ,
,
把A![]() 代入
代入![]() 中,
中,
得:![]() ,
,
解得:![]() ;
;
(2)∵雙曲線![]() 上點C的縱坐標為3,
上點C的縱坐標為3,
∴點C的橫坐標為![]() ,
,
設過AC直線的解析式為![]() ,
,
把A![]() ,C
,C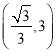 代入
代入![]() 中,
中,
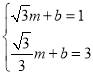 ,
,
解得: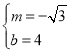 ,
,
∴![]() ,
,
設AC與x軸交點為D,
令y=0,
∴![]() ,
,
解得:![]() ,
,
∴點D的坐標為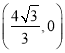 ,
,
∴![]() ;
;
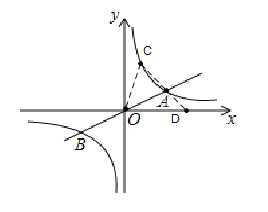
(3)四邊形OMNP是菱形,∠MOP=60°,
設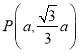 ,則
,則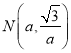 ,
,
∴![]() ,得
,得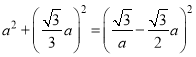 ,
,
解得:![]() ,
,
∴P點坐標為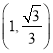 或
或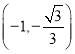 .
.


科目:初中數學 來源: 題型:
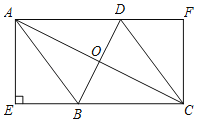
【題目】如圖,在菱形ABCD中,對角線AC,BD交于點O,AE⊥BC交CB延長線于點E,CF∥AE交AD延長線于點F.
(1)求證:四邊形AECF是矩形;
(2)連接OE,若AE=12,AD=13,則線段OE的長度是 .
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小學學生較多,為了便于學生盡快就餐,師生約定:早餐一人一份,一份兩樣,一樣一個,食堂師傅在窗口隨機發放(發放的食品價格一樣),食堂在某天早餐提供了豬肉包、面包、雞蛋、油餅四樣食品.
(1)按約定,“小李同學在該天早餐得到兩個油餅”是 事件;(可能,必然,不可能)
(2)請用列表或樹狀圖的方法,求出小張同學該天早餐剛好得到豬肉包和油餅的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
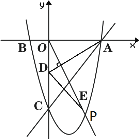
【題目】如圖,拋物線![]() 經過點A(3,0),B(
經過點A(3,0),B(![]() ,0),與y軸交于點C,點P是拋物線在第四象限內的一點.
,0),與y軸交于點C,點P是拋物線在第四象限內的一點.
(1)求拋物線解析式;
(2)點D是線段OC的中點,OP⊥AD,點E是射線OP上一點,OE=AD,求DE的長;
(3)連接CP,AP,是否存在點P,使得OP平分四邊形ABCP的面積?若存在,求點P的坐標;若不存在,說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某軟件開發公司開發了A、B兩種軟件,每種軟件成本均為1400元,售價分別為2000元、1800元,這兩種軟件每天的銷售額共為112000元,總利潤為28000元.
(1)該店每天銷售這兩種軟件共多少個?
(2)根據市場行情,公司擬對A種軟件降價銷售,同時提高B種軟件價格.此時發現,A種軟件每降50元可多賣1件,B種軟件每提高50元就少賣1件.如果這兩種軟件每天銷售總件數不變,那么這兩種軟件一天的總利潤最多是多少?
查看答案和解析>>
科目:初中數學 來源: 題型:
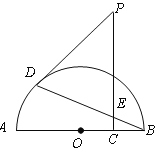
【題目】如圖,點![]() 是半圓
是半圓![]() 的半徑
的半徑![]() 上的動點,作
上的動點,作![]() 于
于![]() .點
.點![]() 是半圓上位于
是半圓上位于![]() 左側的點,連結
左側的點,連結![]() 交線段
交線段![]() 于
于![]() ,且
,且![]() .
.
(1) 求證:![]() 是⊙O的切線.
是⊙O的切線.
(2) 若⊙O的半徑為![]() ,
,![]() ,設
,設![]() .
.
①求![]() 關于
關于![]() 的函數關系式.
的函數關系式.
②當![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
科目:初中數學 來源: 題型:
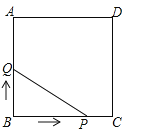
【題目】(3分)如圖,正方形ABCD的邊長為3cm,動點P從B點出發以3cm/s的速度沿著邊BC﹣CD﹣DA運動,到達A點停止運動;另一動點Q同時從B點出發,以1cm/s的速度沿著邊BA向A點運動,到達A點停止運動.設P點運動時間為x(s),△BPQ的面積為y(cm2),則y關于x的函數圖象是( )
A.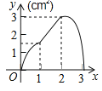 B.
B.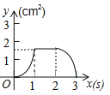 C.
C.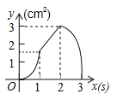 D.
D.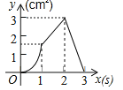
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, 已知點P為⊙O 外一點,PA、PB是⊙O的切線,切點分別是A、B,連接OP交AB于點C,交⊙O于點D,若PA=3cm, ∠APB=60°,則下列結論正確的有( )
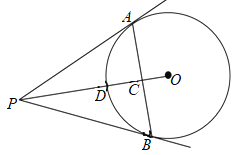
①AB⊥OP;②AC2=PC·OC;③若連接AD,BD,則∠ADB=120°;④PA,PB與劣弧AB圍成的圖形的面積是![]()
A.1個B.2個C.3個D.4個
查看答案和解析>>
科目:初中數學 來源: 題型:
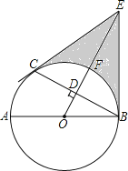
【題目】如圖,AB是⊙O的直徑,C是⊙O上一點,OD⊥BC于點D,過點C作⊙O的切線,交OD的延長線于點E,連接BE.
(1)求證:BE與⊙O相切;
(2)設OE交⊙O于點F,若DF = 2,BC = ![]() ,求陰影部分的面積.
,求陰影部分的面積.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com