
【題目】綜合題
(1)發現
如圖,點 ![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() .
.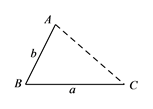
填空:當點 ![]() 位于時,線段
位于時,線段 ![]() 的長取得最大值,且最大值為.(用含
的長取得最大值,且最大值為.(用含 ![]() ,
, ![]() 的式子表示)
的式子表示)
(2)應用
點 ![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() .如圖所示,分別以
.如圖所示,分別以 ![]() ,
, ![]() 為邊,作等邊三角形
為邊,作等邊三角形 ![]() 和等邊三角形
和等邊三角形 ![]() ,連接
,連接 ![]() ,
, ![]() .
.
①找出圖中與 ![]() 相等的線段,并說明理由;
相等的線段,并說明理由;
②直接寫出線段 ![]() 長的最大值.
長的最大值.
(3)拓展
如圖,在平面直角坐標系中,點 ![]() 的坐標為
的坐標為 ![]() ,點
,點 ![]() 的坐標為
的坐標為 ![]()
![]() 為線段
為線段 ![]() 外一動點,且
外一動點,且 ![]() ,
, ![]() ,
, ![]() ,求線段
,求線段 ![]() 長的最大值及此時點
長的最大值及此時點 ![]() 的坐標.
的坐標.
【答案】
(1)CB的延長線上,a+b
(2)解:①DC=BE,理由如下:
∵△ABD和△ACE為等邊三角形,
∴AD=AB,AC=AE,∠BAD=∠CAE=60°,
∴∠BAD+∠BAC=∠CAE+∠BAC,即∠CAD=∠EAB,
∴△CAD≌△EAB.
∴DC=BE.
②BE的最大值是4.
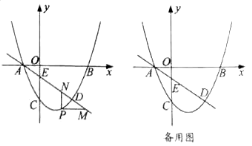
(3)解:如圖3,
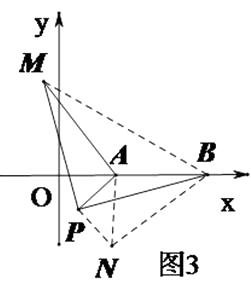
構造△BNP≌△MAP,則NB=AM,由(1)知,當點N在BA的延長線上時,NB有最大值(如備用圖)。
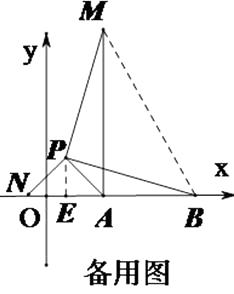
易得△APN是等腰直角三角形,AP=2,∴AN= ![]() ,∴AM=NB=AB+AN=3+
,∴AM=NB=AB+AN=3+ ![]() ;過點P作PE⊥x軸于點E,PE=AE=
;過點P作PE⊥x軸于點E,PE=AE= ![]() ,又A(2,0)∴P(2-
,又A(2,0)∴P(2- ![]() ,
, ![]() )
)
【解析】(1)當點A在線段CB的延長線上時,可得線段AC的長取得最大值為a+b;
(1)根據點A位于CB的延長線上時,線段AC的長取得最大值,即可得到結論。
(2)①根據等邊三角形的性質得到AD=AB,AC=AE,∠BAD=∠CAE=60°,推出△CAD≌△EAB,根據全等三角形的性質得到CD=BE;②由于線段BE長的最大值=線段CD的最大值,根據(1)中的結論即可得到結果。
(3)連接BM,將△APM繞著點P順時針旋轉90°得到△PBN,連接AN,得到△APN是等腰直角三角形,根據全等三角形的性質得PN=PA=2,BN=AM,根據當N在線段BA的延長線時,線段BN取得最大值,即可得到最大值;如圖2,過P作PE⊥x軸于E,根據等腰直角三角形的性質即可得到結論.


 通城學典默寫能手系列答案
通城學典默寫能手系列答案 金牌教輔培優優選卷期末沖刺100分系列答案
金牌教輔培優優選卷期末沖刺100分系列答案科目:初中數學 來源: 題型:
【題目】使(x2+px+8)(x2﹣3x+q)乘積中不含x2與x3項的p、q的值是( )
A.p=0,q=0
B.p=3,q=1
C.p=﹣3,q=﹣9
D.p=﹣3,q=1
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖, ![]() 的一邊
的一邊 ![]() 為平面鏡,
為平面鏡, ![]() ,在
,在 ![]() 上有一點
上有一點 ![]() ,從
,從 ![]() 點射出一束光線經
點射出一束光線經 ![]() 上一點
上一點 ![]() 反射,反射光線
反射,反射光線 ![]() 恰好與
恰好與 ![]() 平行,則
平行,則 ![]() 的度數是( )
的度數是( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,A,B分別為x軸、y軸正半軸上兩動點,∠BAO的平分線與∠OBA的外角平分線所在直線交于點C,則∠C的度數隨A,B運動的變化情況正確的是( )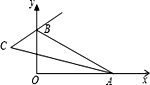
A.點B不動,在點A向右運動的過程中,∠C的度數逐漸減小
B.點A不動,在點B向上運動的過程中,∠C的度數逐漸減小
C.在點A向左運動,點B向下運動的過程中,∠C的度數逐漸增大
D.在點A,B運動的過程中,∠C的度數不變
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】我國魏晉時期的數學家劉徽創立了“割圓術”,認為圓內接正多邊形邊數無限增加時,周長就越接近圓周長,由此求得了圓周率![]() 的近似值.設半徑為
的近似值.設半徑為![]() 的圓內接正
的圓內接正![]() 邊形的周長為
邊形的周長為![]() ,圓的直徑為
,圓的直徑為![]() .如右圖所示,當
.如右圖所示,當![]() 時,
時,![]() ,那么當
,那么當![]() 時,
時,![]() .(結果精確到
.(結果精確到![]() ,參考數據:
,參考數據:![]() )
)

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分10分)
如圖,拋物線![]() 經過點
經過點![]() ,
,![]() ,直線
,直線![]()
![]() 交
交![]() 軸于點
軸于點![]() ,且與拋物線交于
,且與拋物線交于![]() ,
,![]() 兩點.
兩點.![]() 為拋物線上一動點(不與
為拋物線上一動點(不與![]() ,
,![]() 重合).
重合).
(1)求拋物線的解析式;
(2)當點![]() 在直線
在直線![]() 下方時,過點
下方時,過點![]() 作
作![]() 軸交
軸交![]() 于點
于點![]() ,
,![]() 軸交
軸交![]() 于點
于點![]() .求
.求![]() 的最大值;
的最大值;
(3)設![]() 為直線
為直線![]() 上的點,以
上的點,以![]() ,
,![]() ,
,![]() ,
,![]() 為頂點的四邊形能否構成平行四邊形?若能,求出點
為頂點的四邊形能否構成平行四邊形?若能,求出點![]() 的坐標;若不能,請說明理由.
的坐標;若不能,請說明理由.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(本題滿分8分)
如圖,直線![]() 與雙曲線
與雙曲線![]() (
(![]() 為常數,
為常數,![]() )在第一象限內交于點
)在第一象限內交于點![]() ,且與
,且與![]() 軸、
軸、![]() 軸分別交于
軸分別交于![]() ,
,![]() 兩點.
兩點.
(1)求直線和雙曲線的解析式;
(2)點![]() 在
在![]() 軸上,且
軸上,且![]() 的面積等于
的面積等于![]() ,求
,求![]() 點的坐標.
點的坐標.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】下列說法不正確的是( )
A.“某射擊運動員射擊一次,正中靶心”屬于隨機事件
B.“13名同學至少有兩名同學的出生月份是相同的”屬于必然事件
C.“在標準大氣壓下,當溫度降到-5℃時,水結成冰”屬于隨機事件
D.“某袋中有8個質地均勻的球,且都是紅球,任意摸出一球是白球”屬于不可能事件
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com