
【題目】 如圖,在平面直角坐標(biāo)系中,直線y1=kx+b與x軸交于點A(4,0),與y軸交于點B(0,3),點C是直線y2=![]() x+5上的一個動點,連接BC,過點C作CD⊥AB于點D.
x+5上的一個動點,連接BC,過點C作CD⊥AB于點D.
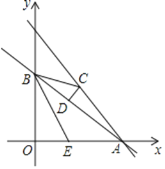
(1)求直線y1=kx+b的函數(shù)表達式;
(2)當(dāng)BC∥x軸時,求BD的長;
(3)點E在線段OA上,OE=![]() OA,當(dāng)點D在第一象限,且△BCD中有一個角等于∠OEB時,請直接寫出點C的橫坐標(biāo).
OA,當(dāng)點D在第一象限,且△BCD中有一個角等于∠OEB時,請直接寫出點C的橫坐標(biāo).
【答案】(1)![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]() .
.
【解析】
(1)把A、B兩點坐標(biāo)代入y1=kx+b,求出a,b的值即可解決問題;
(2)求出點C的坐標(biāo),求出直線CD的解析式,構(gòu)建方程組確定交點坐標(biāo)即可.
(3)分兩種情形:當(dāng)∠BCD=∠BEO時,過點A作AM⊥BC交BC的延長線于M,點M作MN⊥x軸于N.當(dāng)∠CBD=∠BEO時,同法可得點C的橫坐標(biāo).
(1)把A(4,0),B(0,3)代入y1=kx+b,
得到![]() ,
,
解得: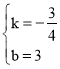 ,
,
∴y1=﹣![]() x+3.
x+3.
(2)∵BC∥x軸,
∴點C的縱坐標(biāo)為3,
當(dāng)y=3時,3=﹣![]() x+5,
x+5,
解得x=![]() ,
,
∴C(![]() ,3),
,3),
∵CD⊥AB,
∴直線CD的解析式為y=![]() x+
x+![]() ,
,
由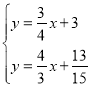 ,解得
,解得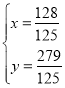 ,
,
∴D(![]() ,
,![]() ),
),
∴BD=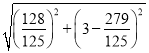 =
=![]() .
.
(3)如圖,當(dāng)∠BCD=∠BEO時,過點A作AM⊥BA交BC的延長線于M,過點M作MN⊥x軸于N.
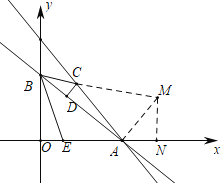
∵OB=3,OE=![]() OA=
OA=![]() ,
,
∴tan∠BEO=![]() =2,
=2,
∵CD⊥AB,AM⊥AB,
∴CD∥AM,
∴∠AMB=∠BCD=∠BEO,
∴tan∠AMB=![]() =2,
=2,
∵AB=![]() =
=![]() =5,
=5,
∴AM=![]() AB=
AB=![]() ,
,
∵∠AOB=∠ANM=∠BAM=90°,
∴∠BAO+∠ABO=90°,∠BAO+∠MAN=90°,
∴∠MAN=∠ABO,
∴△ABO∽△MAN,
∴![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() =
=![]() ,
,
∴AN=![]() ,MN=2,
,MN=2,
∴M(![]() ,2),
,2),
∴直線BM的解析式為y=﹣![]() x+3,
x+3,
由 ,解得x=
,解得x=![]() ,
,
∴點C的橫坐標(biāo)為![]()
如圖,當(dāng)∠CBD=∠BEO時,過點A作AM⊥BA交BC的延長線于M,過點M作MN⊥x軸于N.
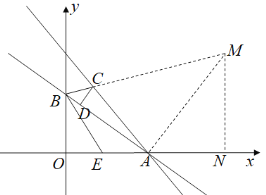
同法可得AM=10,AN=6,MN=8,
∴ON=10,
∴M(10,8),
∴直線BM的解析式為y=![]() x+3,
x+3,
由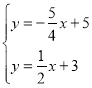 ,解得x=
,解得x=![]() ,
,
∴點C的橫坐標(biāo)為![]()
綜上所述,點C的橫坐標(biāo)為![]() 或
或![]() .
.


 閱讀快車系列答案
閱讀快車系列答案科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,一次函數(shù)![]() 的圖象與反比例函數(shù)
的圖象與反比例函數(shù)![]() 的圖象交于點
的圖象交于點![]() 和點C,與y軸交于點B,
和點C,與y軸交于點B,![]() 的面積是6.
的面積是6.
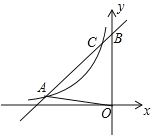
(1)求一次函數(shù)與反比例函數(shù)的表達式;(2)當(dāng)![]() 時,比較
時,比較![]() 與
與![]() 的大小.
的大小.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,點![]() 是坐標(biāo)原點,點
是坐標(biāo)原點,點![]() 是反比例函數(shù)
是反比例函數(shù)![]()
![]() 圖像上一點,點
圖像上一點,點![]() 在
在![]() 軸上,
軸上,![]() ,四邊形
,四邊形![]() 是平行四邊形,
是平行四邊形,![]() 交反比例函數(shù)
交反比例函數(shù)![]()
![]() 圖像于點
圖像于點![]() .
.
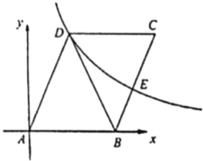
(1)平行四邊形![]() 的面積等于______;
的面積等于______;
(2)設(shè)![]() 點橫坐標(biāo)為
點橫坐標(biāo)為![]() ,試用
,試用![]() 表示點
表示點![]() 的坐標(biāo);(要有推理和計算過程)
的坐標(biāo);(要有推理和計算過程)
(3)求![]() 的值;
的值;
(4)求![]() 的最小值.
的最小值.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】某街道組織志愿者活動,選派志愿者到小區(qū)服務(wù).若每一個小區(qū)安排4人,那么還剩下78人;若每個小區(qū)安排8人,那么最后一個小區(qū)不足8人,但不少于4人.求這個街道共選派了多少名志愿者?
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
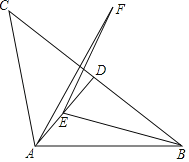
【題目】 如圖,△ABC中,AB=AC,∠ABC=α,tanα=![]() ,AD⊥BC于點D,點E是線段AD上的一個動點,連接EB,將線段EB繞點E逆時針旋轉(zhuǎn)2α后得到線段EF,連接AF,若BC=24,則線段AF的最小值為_____.
,AD⊥BC于點D,點E是線段AD上的一個動點,連接EB,將線段EB繞點E逆時針旋轉(zhuǎn)2α后得到線段EF,連接AF,若BC=24,則線段AF的最小值為_____.
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,是某公園一圓形噴水池,在池中心豎直安裝一根水管OA=1.25m,A處是噴頭,水流在各個方向沿形狀相同的拋物線落下,水落地后形成一個圓,圓心為O,直徑為線段CB.建立如圖所示的平面直角坐標(biāo)系,若水流路線達到最高處時,到x軸的距離為2.25m,到y軸的距離為1m,則水落地后形成的圓的直徑CB=_____m.

查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】如圖,矩形ABCD中,AB=2,AD=3.E,F分別是AD,CD上的動點,EF=2.Q是EF的中點,P為BC上的動點,連接AP,PQ.則AP+PQ的最小值等于( )
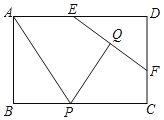
A.2B.3C.4D.5
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
【題目】下列計算:①![]() ;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中錯誤的個數(shù)是( )
;②(x﹣2y)2=x2﹣4y2;③(﹣a)4a3=﹣a7;④x10÷x5=x2,其中錯誤的個數(shù)是( )
A.1B.2C.3D.4
查看答案和解析>>
科目:初中數(shù)學(xué) 來源: 題型:
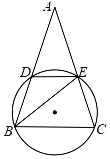
【題目】如圖,等腰△ABC兩腰AB,AC分別交⊙O于點D,E,點A在⊙O外,點B,C在⊙O上(不與D,E重合),連結(jié)BE,DE.已知∠A=∠EBC,設(shè)![]() =k(0<k<1).
=k(0<k<1).
(1)若∠A=50°,求![]() 的度數(shù);
的度數(shù);
(2)若k=![]() ,求
,求![]() 的值;
的值;
(3)設(shè)△ABC,△ADE,△BEC的周長分別為c,c1,c2,求證:1<![]() ≤
≤![]() .
.
查看答案和解析>>
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com