
【題目】△ABC內接于⊙O,AB=AC,BD⊥AC,垂足為點D,交⊙O于點E,連接AE.
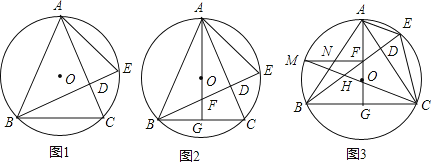
(1)如圖1,求證:∠BAC=2∠CAE;
(2)如圖2,射線AO交線段BD于點F,交BC邊于點G,連接CE,求證:BF=CE;
(3)如圖3,在(2)的條件下,連接CO并延長,交線段BD于點H,交⊙O于點M,連接FM,交AB邊于點N,若BH=DH,四邊形BHOG的面積為5![]() ,求線段MN的長.
,求線段MN的長.
【答案】(1)見詳解;(2)見詳解;(3)![]()
【解析】
(1)先依據等腰三角形的性質和三角形的內角和定理證明∠BAC+2∠C=180°,然后得到2∠CAE+2∠E=180°,然后根據同弧所對的圓周角相等得到∠E=∠C,即可得到結論;
(2)連接OB、OC.先依據SSS證明△ABO≌△ACO,從而得到∠BAO=∠CAO,然后在依據ASA證明△ABF≌△ACE,最后根據全等三角形的性質可證明BF=CE;
(3)連接HG、BM.由三線合一的性質證明BG=CG,從而得到HG是△BCD的中位線,則∠FHO=∠AFD=∠HFO,于是可得到HO=OF,然后得到∠OGH=∠OHG,從而得到OH=OG,則OF=OG,接下來證明四邊形MFGB是矩形,然后由MF∥BC證明△MFH∽△CBH,從而可證明HF=FD.接下來再證明△ADF≌△GHF,由全等三角形的性質的到AF=FG,然后再證明△MNB≌△NAF,于是得到MN=NF.設S△OHF=S△OHG=a,則S△FHG=2a,S△BHG=4a,然后由S四邊形BHOG=5![]() ,可求得a=
,可求得a=![]() ,設HF=x,則BH=2x,然后證明△GFH∽△BFG,由相似三角形的性質可得到HG=
,設HF=x,則BH=2x,然后證明△GFH∽△BFG,由相似三角形的性質可得到HG=![]() x,然后依據S△BHG=
x,然后依據S△BHG=![]() BHHG=4
BHHG=4![]() ,可求得x=2,故此可得到HB、GH的長,然后依據勾股定理可求得BG的長,于是容易求得MN的長.
,可求得x=2,故此可得到HB、GH的長,然后依據勾股定理可求得BG的長,于是容易求得MN的長.
解:(1)∵AB=AC,
∴∠ABC=∠ACB.
∴∠BAC+2∠C=180°.
∵BD⊥AC,
∴∠ADE=90°.
∴∠E+∠CAE=90°.
∴2∠CAE+2∠E=180°.
∵∠E=∠ACB,
∴2∠CAE+2∠ACB=180°.
∴∠BAC=2∠CAE.
(2)連接OB、OC.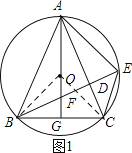
∵AB=AC,AO=AO,OB=OC,
∴△ABO≌△ACO.
∴∠BAO=∠CAO.
∵∠BAC=2∠CAE,
∴∠BAO=∠CAE.
在△ABF和△ACE中,
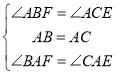 ,
,
∴△ABF≌△ACE.
∴BF=CE.
(3)連接HG、BM.
∵AB=AC,∠BAO=∠CAO,
∴AG⊥BC,BG=CG.
∵BH=DH,
∴HG是△BCD的中位線.
∴HG∥CD.
∴∠GHF=∠CDE=90°.
∵OA=OC,
∴∠OAC=∠OCA.
∵∠OAC+∠AFD=90°,∠OCA+∠FHO=90°,
∴∠FHO=∠AFD=∠HFO.
∴HO=OF.
∵∠HFO+∠OGH=90°,∠OHF+∠OH=90°,
∴∠OGH=∠OHG.
∴OH=OG.
∴OF=OG.
∵OM=OC,
∴四邊形MFCG是平行四邊形.
又∵MC是圓O的直徑,
∴∠CBM=90°.
∴四邊形MFGB是矩形.
∴MB=FG,∠FMB=∠AFN=90°.
∵MF∥BC,
∴△MFH∽△CBH.
∴![]() .
.
∴HF:HD=1:2.
∴HF=FD.
在△ADF和△GHF中,
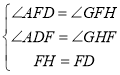 ,
,
∴△ADF≌△GHF.
∴AF=FG.
∴MB=AF.
在△MNB和△NAF中,
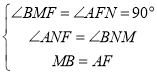 ,
,
∴△MNB≌△NAF.
∴MN=NF.
設S△OHF=S△OHG=a,則S△FHG=2a,S△BHG=4a,
∴S四邊形BHOG=5a=5![]() .
.
∴a=![]() .
.
設HF=x,則BH=2x.
∵∠HHG=∠GFB,∠GHF=∠FGB,
∴△GFH∽△BFG.
∴![]() ,即
,即![]() .
.
∴HG=![]() .
.
∴S△BHG=![]() BHHG=
BHHG=![]() ×2x
×2x![]() =4
=4![]() ,
,
解得:x=2.
∴HB=4,GH=2![]() .
.
由勾股定理可知:BG=2![]() .
.
∴MF=2![]() .
.
∴MN=NF=![]() .
.


科目:初中數學 來源: 題型:
【題目】已知,在![]() 中,
中,![]() ,點
,點![]() 在
在![]() 邊上,點
邊上,點![]() 在
在![]() 邊上,
邊上,![]() ,過點
,過點![]() 作
作![]() 交
交![]() 的延長線于點
的延長線于點![]() .
.
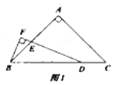
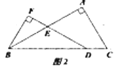
(1)如圖1,當![]() 時:①
時:①![]() 的度數為__________;②求證;
的度數為__________;②求證;![]() ;
;
(2)如圖2,當![]() 時,求
時,求![]() 的值(用含
的值(用含![]() 的式子表示).
的式子表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某商場秋季計劃購進一批進價為每件40元的![]() 恤進行銷售.
恤進行銷售.
(1)根據銷售經驗,應季銷售時,若每件![]() 恤的售價為60元,可售出400件;若每件
恤的售價為60元,可售出400件;若每件![]() 恤的售價每提高1元,銷售量相應減少10件.
恤的售價每提高1元,銷售量相應減少10件.
①假設每件![]() 恤的售價提高
恤的售價提高![]() 元,那么銷售每件
元,那么銷售每件![]() 恤所獲得的利潤是 元,銷售量是 件(用含
恤所獲得的利潤是 元,銷售量是 件(用含![]() 的代數式表示);
的代數式表示);
②設應季銷售利潤為![]() 元,請寫
元,請寫![]() 與
與![]() 的函數關系式;并求出應季銷售利潤為8000元時每件
的函數關系式;并求出應季銷售利潤為8000元時每件![]() 恤的售價.
恤的售價.
(2)根據銷售經驗,過季處理時,若每件![]() 恤的售價定為30元虧本銷售,可售出50件;若每件
恤的售價定為30元虧本銷售,可售出50件;若每件![]() 恤的售價每降低1元,銷售量相應增加5條.
恤的售價每降低1元,銷售量相應增加5條.
①若剩余100件![]() 恤需要處理,經過降價處理后還是無法銷售的只能積壓在倉庫,損失本金;若使虧損金額最小,每件
恤需要處理,經過降價處理后還是無法銷售的只能積壓在倉庫,損失本金;若使虧損金額最小,每件![]() 恤的售價應是多少元?
恤的售價應是多少元?
②若過季需要處理的![]() 恤共
恤共![]() 件,且
件,且![]() ,季虧損金額最小是 元(用含
,季虧損金額最小是 元(用含![]() 的代數式表示).
的代數式表示).
查看答案和解析>>
科目:初中數學 來源: 題型:
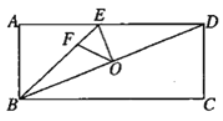
【題目】如圖,O為矩形ABCD的對角線BD的中點,點E在AD上,連接EB、EO,BD平分∠EBC,點F在BE上,tan∠OFE=tan∠ABD,若AE=3EF,CD=3,則OD的長為______.
查看答案和解析>>
科目:初中數學 來源: 題型:
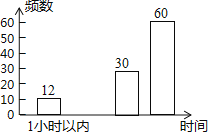
【題目】某市教育主管部門為了解學生的作業量情況,隨機抽取了幾所中學八年級的部分學生進行了一次調查,并根據收集到的信息進行了統計,繪制了下面兩幅尚不完整的統計圖.請你根據統計圖、表中所提供的信息解答下列問題:
(1)本次共抽取了 名學生進行調查;
(2)x= ,y= ,補全條形統計圖;
(3)若這幾所中學八年級的學生共有3200人,請估計做作業時間在2小時以上的學生人數是多少?
(4)由圖表可知,這次被調查的八年級學生的作業時間的中位數一定落在1.5小時﹣2小時這一時段內,你認為這種判斷正確嗎?(不需要說明理由)
寫作業時間 | 頻數 | 頻率 |
1小時以內 | 12 | 0.1 |
1﹣1.5 | x | 0.15 |
1.5﹣2 | 30 | 0.25 |
2小時以上 | 60 | y |
查看答案和解析>>
科目:初中數學 來源: 題型:
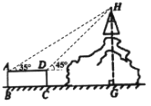
【題目】如圖,山上有一座高塔,山腳下有一圓柱形建筑物平臺,高塔及山的剖面與圓柱形建筑物平臺的剖面ABCD在同一平面上,在點A處測得塔頂H的仰角為35°,在點D處測得塔頂H的仰角為45°,又測得圓柱形建筑物的上底面直徑AD為6m,高CD為2.8m,則塔頂端H到地面的高度HG為( )
(參考數據:![]() ,
,![]() ,
,![]() ,
,![]() )
)
A.10.8mB.14mC.16.8mD.29.8m
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】![]() 城有肥料
城有肥料![]() ,
,![]() 城有肥料
城有肥料![]() .現要把這些肥料全部運往
.現要把這些肥料全部運往![]() 、
、![]() 兩鄉,
兩鄉,![]() 鄉需要肥料240t,
鄉需要肥料240t,![]() 鄉需要肥料
鄉需要肥料![]() ,其運往
,其運往![]() 、
、![]() 兩鄉的運費如下表:
兩鄉的運費如下表:
兩城/兩鄉 | C/(元/ | D/(元/ |
| 20 | 24 |
| 15 | 17 |
設從![]() 城運往
城運往![]() 鄉的肥料為
鄉的肥料為![]() ,從
,從![]() 城運往兩鄉的總運費為
城運往兩鄉的總運費為元,從
![]() 城運往兩鄉的總運費為
城運往兩鄉的總運費為![]() 元
元
(1)分別寫出![]() 、
、![]() 與
與![]() 之間的函數關系式(不要求寫自變量的取值范圍);
之間的函數關系式(不要求寫自變量的取值范圍);
(2)試比較![]() 、
、![]() 兩城總運費的大小;
兩城總運費的大小;
(3)若![]() 城的總運費不得超過4800元,怎樣調運使兩城總費用的和最少?并求出最小值.
城的總運費不得超過4800元,怎樣調運使兩城總費用的和最少?并求出最小值.
查看答案和解析>>
科目:初中數學 來源: 題型:
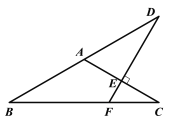
【題目】如圖,在△ABC中,AB=AC,∠BAC=120°,線段AC的垂直平分線交BC于點F,交AC于點E,交BA的延長線于點D.若DE=3,則BF=( ).
A.4B.3C.2D.![]()
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com