
【題目】某個體小服裝店主準備在夏季來臨前,購進甲、乙兩種T恤.兩種T恤的相關信息如表:
品牌 | 甲 | 乙 |
進價(元/件) | 45 | 80 |
售價(元/件) | 75 | 120 |
根據上述信息,該店決定用不少于6198元,但不超過6296元的資金購進這兩種T恤共100件請解答下列問題:
(1)該店有哪幾種進貨方案?
(2)該店按哪種方案進貨所獲利潤最大,最大利潤是多少?
【答案】(1)有三種進貨方案,方案一:購進甲種T恤49件,乙種T恤51件;方案二:購進甲種T恤50件,乙種T恤50件;方案三:購進甲種T恤51件,乙種T恤49件;(2)方案一該店購進甲種T恤49件,乙種T恤51件時獲利最大,最大利潤為3510元.
【解析】
(1)設購進甲種T恤x件,則購進乙種T恤(100﹣x)件,根據總價=單價×數量結合總價不少于6198元且不超過6296元,即可得出關于x的一元一次不等式組,解之即可得出x的取值范圍,再結合x為整數即可得出各進貨方案;
(2)設所獲得利潤為W元,根據總利潤=每件的利潤×銷售數量(購進數量),即可得出W關于x的函數關系式,再利用一次函數的性質即可解決最值問題.
解:(1)設購進甲種T恤x件,則購進乙種T恤(100﹣x)件.
依題意,得:![]() ,
,
解得:48![]() ≤x≤51
≤x≤51![]() .
.
∵x為正整數,
∴x=49,50,51.
∴有三種進貨方案,方案一:購進甲種T恤49件,乙種T恤51件;方案二:購進甲種T恤50件,乙種T恤50件;方案三:購進甲種T恤51件,乙種T恤49件.
(2)設所獲得利潤為W元.
依題意,得:W=(75﹣45)x+(120﹣80)(100﹣x)=﹣10x+4000.
∵k=﹣10<0,
∴W值隨x值的增大而減小,
∴當x=49時,W取得最大值,最大值=﹣10×49+4000=3510.
答:方案一該店購進甲種T恤49件,乙種T恤51件時獲利最大,最大利潤為3510元.


科目:初中數學 來源: 題型:
【題目】一輛汽車在某次行駛過程中,油箱中的剩余油量y(升)與行駛路程x(千米)之間是一次函數關系,其部分圖象如圖所示.
(1)求y關于x的函數關系式;(不需要寫定義域)
(2)已知當油箱中的剩余油量為8升時,該汽車會開始提示加油,在此次行駛過程中,行駛了500千米時,司機發現離前方最近的加油站有30千米的路程,在開往該加油站的途中,汽車開始提示加油,這時離加油站的路程是多少千米?

查看答案和解析>>
科目:初中數學 來源: 題型:
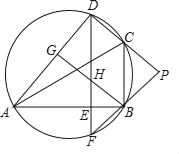
【題目】如圖,D是△ABC外接圓上的點,且B,D位于AC的兩側,DE⊥AB,垂足為E,DE的延長線交此圓于點F.BG⊥AD,垂足為G,BG交DE于點H,DC,FB的延長線交于點P,且PC=PB.
(1)求證:∠BAD=∠PCB;
(2)求證:BG∥CD;
(3)設△ABC外接圓的圓心為O,若AB=![]() DH,∠COD=23°,求∠P的度數.
DH,∠COD=23°,求∠P的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
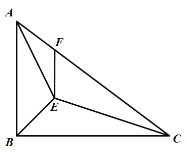
【題目】如圖,在Rt△ABC中,∠ABC=90°,AB=6,BC=8,點E是△ABC的內心,過點E作EF∥AB交AC于點F,則EF的長為( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】隨著移動互聯網的快速發展,基于互聯網的共享單車應運而生.為了解某小區居民使用共享單車的情況,某研究小組隨機采訪該小區的![]() 位居民,得到這
位居民,得到這![]() 位居民一周內使用共享單車的次數分別為:
位居民一周內使用共享單車的次數分別為:![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)這組數據的中位數是________,眾數是________;
(2)計算這![]() 位居民一周內使用共享單車的平均次數;
位居民一周內使用共享單車的平均次數;
(3)若該小區有![]() 名居民,試估計該小區居民一周內使用共享單車的總次數.
名居民,試估計該小區居民一周內使用共享單車的總次數.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com