
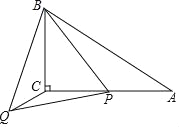
【題目】如圖,在△ABC中,∠ACB=90°,∠A=30°,AB=5,點P是AC上的動點,連接BP,以BP為邊作等邊△BPQ,連接CQ,則點P在運動過程中,線段CQ長度的最小值是______.
科目:初中數學 來源: 題型:
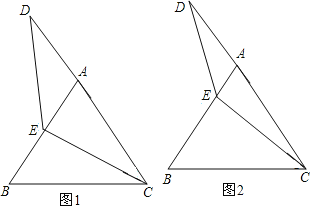
【題目】等邊△ABC中,點E在AB上,點D在CA的延長線上,且ED=EC.試探索以下問題:
(1)如圖1,當E為AB中點時,試確定線段AD與BE的大小關系,請你直接寫出結論:AD BE;
(2)如圖2,若點E為線段AB上任意一點,(1)中結論是否成立,若成立,請證明結論,若不成立,請說明理由。
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在Rt△ABC 中,∠C=90°,沿過點A的一條直線AE折疊Rt△ABC,使點C恰好落在AB邊的中點D處,則∠B的度數是( )

A. 25° B. 30° C. 40° D. 45°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】補全下列解題過程:
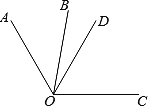
如圖,OD是∠AOC的平分線,且∠BOC-∠AOB=40°,若∠AOC=120°,求∠BOD的度數.
解:∵OD是∠AOC的平分線,∠AOC=120°
∴∠DOC=![]() ∠_______=______°.
∠_______=______°.
∵∠BOC+∠_____=120°,∠BOC-∠AOB=40°
∴∠BOC=80°
∴∠BOD=∠BOC-∠______=______°
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】已知兩個等腰直角△ABC和△CDE,它們的兩個直角頂點B、D在直線MN上,過點A、E分別作AG⊥MN,EF⊥MN,垂足分別為G、F.
(1)如圖1,當△ABC和△CDE在△BCD的外部時,請你探索線段EF、DB、AG之間的數量關系,其數量關系為______.
(2)如圖2,將圖1中的△ABC沿BC翻折,其他條件不變,那么(1)中的結論是否仍然成立?若成立,請你給出證明,若不成立,請探索它們的數量關系,并說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】(定義)數學課上,陳老師對我們說,如果1條線段將一個三角形分成2個等腰三角形,那么這1條線段就稱為這個三角形的“好線”,如果2條線段將一個三角形分成3個等腰三角形,那么這2條線段就稱為這個三角形的“好好線”.
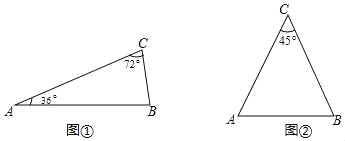
(理解)如圖①,在△ABC中,∠A=36°,∠C=72°,請你在這個三角形中畫出它的“好線”,并標出等腰三角形頂角的度數.
如圖②,已知△ABC是一個頂角為45°的等腰三角形,請你在這個三角形中畫出它的“好好線”,并標出所分得的等腰三角形底角的度數.
(應用)
(1)在△ABC中,已知一個內角為42°,若它只有“好線”,請你寫出這個三角形最大內角的所有可能值______;
(2)在△ABC中,∠C=27°,AD和DE分別是△ABC的“好好線”,點D在BC邊上,點E在AB邊上,且AD=DC,BE=DE,請你根據題意畫出示意圖,并求∠B的度數.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,四邊形ABCD中,AC=a,BD=b,且AC⊥BD,順次連接四邊形ABCD各邊的中點,得到四邊形A1B1C1D1,再順次連接四邊形A1B1C1D1各邊的中點,得到四邊形A2B2C2D2;…;如此進行下去,得到四邊形A7B7C7D7,那么四邊A7B7C7D7形的周長為______.

查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com