
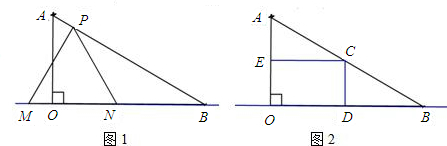
如圖1,在Rt△AOB中,∠AOB=90°,AO= ,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒
,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒 個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
(1)求當等邊△PMN的頂點M運動到與點O重合時t的值.
(2)求等邊△PMN的邊長(用t的代數式表示);
(3)如果取OB的中點D,以OD為邊在Rt△AOB 內部作如圖2所示的矩形ODCE,點C在線段AB上.設等邊△PMN和矩形ODCE重疊部分的面積為S,請求出當0≤t≤2秒時S與t的函數關系式,并求出S的最大值.
(4)在(3)中,設PN與EC的交點為R,是否存在點R,使△ODR是等腰三角形?若存在,求出對應的t的值;若不存在,請說明理由.
解:(1)當等邊△PMN的頂點M運動到與點O重合時,
MP⊥AB,∵∠A=60°,∴AP=4 ,∴
,∴ 。(2分)
。(2分)
(2)∵AP=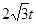 ,∴BP=
,∴BP=
又∵∠B=30°,∠PMB=600°,∴∠BPM=90°
tan∠B=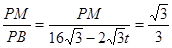
∴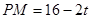 ,即等邊△PMN的邊長為
,即等邊△PMN的邊長為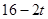 .(4分)
.(4分)
(3)①當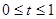 時,如圖AP=
時,如圖AP=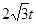 ,∴
,∴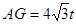
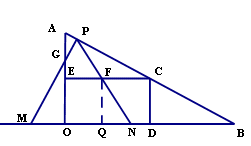
∴ ,∴
,∴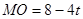 ,
,
∴ .
.
過F作FQ⊥0B于Q,則QN=4,∴EF=OQ= .
.
等邊△PMN和矩形ODCE重疊部分的面積為四邊形EFNO的面積,設為S1,
∴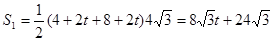
∵ >0,∴S1隨t的增大而增大,
>0,∴S1隨t的增大而增大,
∴t=1時,,∴S1的最大值為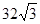 .(7分)
.(7分)
②當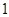 <t<2時,如圖
<t<2時,如圖
在△EGK中,GE=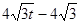 ,∴EK=
,∴EK= ,
,
∴S△GEK= .
.
∴等邊△PMN和矩形ODCE重疊部分的面積為四邊形EFNO的面積與△EGK的面積差,設為S2,
∴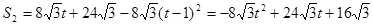 .
.
∵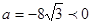 ,對稱軸為
,對稱軸為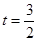 ,
,
∴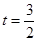 時,
時, 的最大值為
的最大值為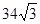 .(9分)
.(9分)
當 時,
時,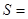
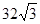 。
。
綜上可知:當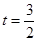 時,S的最大值為
時,S的最大值為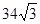 .(10分)
.(10分)
(4)過R作RH⊥OB于H,RH= ,HN=4,
,HN=4,
OH= ,OD=12,DH=
,OD=12,DH=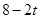 ,
,
①OR=OD=12時, ,
,
∴ ,
,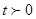 ,∴
,∴ >2,不合題意舍去。
>2,不合題意舍去。
②DR=OD=12時,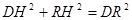 ,
,
∴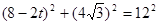 ,∴
,∴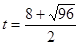 >2,或
>2,或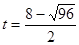 <0,都不合題意舍去。
<0,都不合題意舍去。
③OR=DR時,H為CD中點,OH=6,∴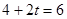 ,∴
,∴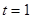 。
。
綜上所述,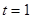 時,△ODR是等腰三角形。(12分)
時,△ODR是等腰三角形。(12分)
解析


 名校課堂系列答案
名校課堂系列答案科目:初中數學 來源: 題型:
| 3 |
| 3 |
查看答案和解析>>
科目:初中數學 來源: 題型:

查看答案和解析>>
科目:初中數學 來源:2011-2012學年重慶全善學校九年級下學期第二次月考數學試卷(解析版) 題型:解答題
如圖1,在Rt△AOB中,∠AOB=90°,AO= ,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒
,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒 個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
(1)求當等邊△PMN的頂點M運動到與點O重合時t的值.
(2)求等邊△PMN的邊長(用t的代數式表示);
(3)如果取OB的中點D,以OD為邊在Rt△AOB 內部作如圖2所示的矩形ODCE,點C在線段AB上.設等邊△PMN和矩形ODCE重疊部分的面積為S,請求出當0≤t≤2秒時S與t的函數關系式,并求出S的最大值.
(4)在(3)中,設PN與EC的交點為R,是否存在點R,使△ODR是等腰三角形?若存在,求出對應的t的值;若不存在,請說明理由.

查看答案和解析>>
科目:初中數學 來源: 題型:解答題
 ,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒
,∠ABO=30°.動點P在線段AB上從點A向終點B以每秒 個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
個單位的速度運動,設運動時間為t秒.在直線OB 上取兩點M、N作等邊△PMN.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com