
【題目】如圖,平行四邊形![]() 中,
中,![]() 是對角線
是對角線![]() 的中點,過點
的中點,過點![]() 的直線
的直線![]() 分別交
分別交![]() ,
,![]() 的延長線于
的延長線于![]() ,
,![]() .
.
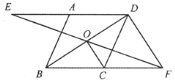
(1)求證:![]() ;
;
(2)若![]() ,試探究線段
,試探究線段![]() 與線段
與線段![]() 之間的關系,并說明理由.
之間的關系,并說明理由.
【答案】(1)見解析;(2)OC∥DF,且OC=![]() DF,理由見解析.
DF,理由見解析.
【解析】
(1)由平行四邊形的性質得出AD∥BC,AD=BC,得出∠ADB=∠CBD,證明△BOF≌△DOE,得出DE=BF,即可得出結論;
(2)證出CF=BC,得出OC是△BDF的中位線,由三角形中位線定理即可得出結論.
(1)證明:∵四邊形ABCD是平行四邊形,
∴AD∥BC,AD=BC,
∴∠ADB=∠CBD,
∵O是對角線BD的中點,
∴OB=OD,
在△BOF和△DOE中,
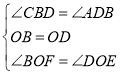 ,
,
∴△BOF≌△DOE(ASA),
∴DE=BF,
∴DE=AD=BF﹣BC,
∴AE=CF;
(2)解:OC∥DF,且OC=![]() DF,理由如下:
DF,理由如下:
∵AE=BC,AE=CF,
∴CF=BC,
∵OB=OD,
∴OC是△BDF的中位線,
∴OC∥DF,且OC=![]() DF.
DF.


科目:初中數學 來源: 題型:
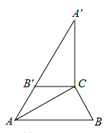
【題目】如圖,在Rt△ABC中,∠ACB=90°,∠B=60°,BC=2,△A′B′C可以由△ABC繞點C順時針旋轉得到,其中點A′與點A是對應點,點B′與點B是對應點,連接AB′,且A、B′、A′在同一條直線上,則AA′的長為______
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,二次函數y=ax2+bx+c(a≠0)的圖象經過點A,B,C.現有下面四個推斷:①拋物線開口向下;②當x=-2時,y取最大值;③當m<4時,關于x的一元二次方程ax2+bx+c=m必有兩個不相等的實數根;④直線y=kx+c(k≠0)經過點A,C,當kx+c> ax2+bx+c時,x的取值范圍是-4<x<0;其中推斷正確的是 ( )
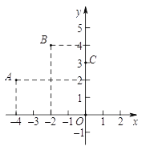
A. ①②B. ①③C. ①③④D. ②③④
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,從地面上的點A看一山坡上的電線桿PQ,測得桿頂端點P的仰角是45°,向前走6m到達B點,測得桿頂端點P和桿底端點Q的仰角分別是60°和30°.
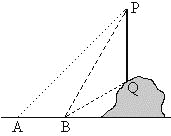
(1)求∠BPQ的度數;
(2)求該電線桿PQ的高度(結果精確到1m).備用數據:![]() ,
,![]()
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在平面直角坐標系中,矩形![]() 的頂點
的頂點![]() 在
在![]() 軸的正半軸上,
軸的正半軸上,![]() .對角線
.對角線![]() 相交于點
相交于點![]() ,反比例函數
,反比例函數![]() 的圖像經過點
的圖像經過點![]() ,分別與
,分別與![]() 交于點
交于點![]() .
.
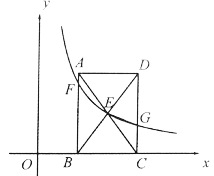
(1)若![]() ,求
,求![]() 的值;
的值;
(2)連接![]() ,若
,若![]() ,求
,求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】平面直角坐標系中,二次函數y=ax2+bx+c(a≠0)的圖象如圖所示,現給出下列結論:①abc<0;②c+2a>0;③9a﹣3b+c=0;④a﹣b≤am2+bm(m為實數);⑤4ac﹣b2<0.其中正確結論的個數是( )

A. 2B. 3C. 4D. 5
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AC=BC,∠ACB=120°,D是AB中點,一個以點D為頂點的60°角繞點D旋轉,使角的兩邊分別與AC、BC的延長線相交,交點分別為點E,F,DF與AC交于點M,DE與BC交于點N.
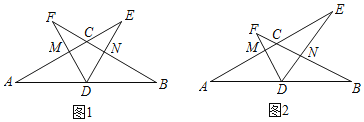
(1)如圖1,若CE=CF,求證:DE=DF;
(2)如圖2,在∠EDF繞點D旋轉的過程中:
①探究三條線段AC,CE,CF之間的數量關系,并說明理由;
②若CE=9,CF=4,求CN的長.
查看答案和解析>>
科目:初中數學 來源: 題型:
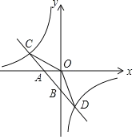
【題目】如圖,已知一次函數y1=k1x+b的圖象與x軸、y軸分別交于A.B兩點,與反比例函數y2=![]() 的圖象分別交于C.D兩點,點D(2,﹣3),OA=2.
的圖象分別交于C.D兩點,點D(2,﹣3),OA=2.
(1)求一次函數y1=k1x+b與反比例函數y2=![]() 的解析式;
的解析式;
(2)直接寫出k1x+b﹣![]() ≥0時自變量x的取值范圍.
≥0時自變量x的取值范圍.
查看答案和解析>>
科目:初中數學 來源: 題型:
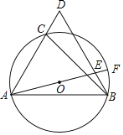
【題目】如圖,點C是等邊△ABD的邊AD上的一點,且∠ACB=75°,⊙O是△ABC的外接圓,連結AO并延長交BD于E、交⊙O于F.
(1)求證:∠BAF=∠CBD;
(2)過點C作CG∥AE交BD于點G,求證:CG是⊙O的切線;
(3)在(2)的條件下,當AF=2![]() 時,求
時,求![]() 的值.
的值.
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com