
【題目】某公園有一個拋物線形狀的觀景拱橋ABC,其橫截面如圖所示,在圖中建立的直角坐標系中,拋物線的解析式為y=﹣![]() +c且過頂點C(0,5)(長度單位:m)
+c且過頂點C(0,5)(長度單位:m)
(1)直接寫出c的值;
(2)現因搞慶典活動,計劃沿拱橋的臺階表面鋪設一條寬度為1.5m的地毯,地毯的價格為20元/m2,求購買地毯需多少元?
(3)在拱橋加固維修時,搭建的“腳手架”為矩形EFGH(H、G分別在拋物線的左右側上),并鋪設斜面EG.已知矩形EFGH的周長為27.5m,求斜面EG的傾斜角∠GEF的度數.(精確到0.1°)

【答案】(1)5;(2)900元;(3)20.6°.
【解析】
(1)根據點在拋物線上易求得c;
(2)根據解析式求出A,B,C三點坐標,求出地毯的總長度,再根據地毯的價格求出購買地毯需要的錢;
(3)由已知矩形EFGH的周長,求出GF,EF邊的長度,再根據三角函數性質求出傾斜角∠GEF的度數.
(1)拋物線的解析式為y=﹣![]() +c,
+c,
∵點(0,5)在拋物線上
∴c=5;
(2)由(1)知,OC=5,
令y=0,即﹣![]() +5=0,解得x1=10,x2=﹣10;
+5=0,解得x1=10,x2=﹣10;
∴地毯的總長度為:AB+2OC=20+2×5=30,
∴30×1.5×20=900
答:購買地毯需要900元.
(3)可設G的坐標為(m,﹣![]() +5)其中m>0
+5)其中m>0
則EF=2m,GF=﹣![]() +5,
+5,
由已知得:2(EF+GF)=27.5,
即2(2m﹣![]() +5)=27.5,
+5)=27.5,
解得:m1=5,m2=35(不合題意,舍去),
把m1=5代入,﹣![]() +5=﹣
+5=﹣![]() ×52+5=3.75,
×52+5=3.75,
∴點G的坐標是(5,3.75),
∴EF=10,GF=3.75,
在Rt△EFG中,tan∠GEF=![]() =0.375,
=0.375,
∴∠GEF≈20.6°.


科目:初中數學 來源: 題型:
【題目】如圖,在△ABC中,AB=AC=4,∠BAC=90°,點D在邊AB上,BE∥CD,AE⊥CD,垂足為F,且EF=2,點G在線段CF上,若∠GAF=45°,則△ACG的面積為_____.

查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】銳銳參加我市電視臺組織的“牡丹杯”智力競答節目,答對最后兩道單選題就順利通關,第一道單選題有3個選項,第二道單選題有4個選項,這兩道題銳銳都不會,不過銳銳還有兩個“求助”可以用(使用“求助”一次可以讓主持人去掉其中一題的一個錯誤選項).
(1)如果銳銳兩次“求助”都在第一道題中使用,那么銳銳通關的概率是________;
(2)如果銳銳兩次“求助”都在第二道題中使用,那么銳銳通關的概率是________;
(3)如果銳銳每道題各用一次“求助”,請用樹狀圖或者列表來分析他順利通關的概率.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,直角坐標系中,![]() 的頂點都在網格點上,其中,C點坐標為
的頂點都在網格點上,其中,C點坐標為![]() .
.
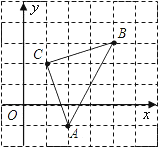
(1)寫出點A、B的坐標:
![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(2)將![]() 先向左平移2個單位長度,再向上平移1個單位長度,得到
先向左平移2個單位長度,再向上平移1個單位長度,得到![]() ,則
,則![]() 的三個頂點坐標分別是
的三個頂點坐標分別是![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]() 、
、![]() ______ ,______
______ ,______ ![]()
(3)求![]() 的面積.
的面積.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】如圖,有![]() 、
、![]() 、
、![]() 三個居民小區的位置成三角形,現決定在三個小區之間修建一個購物超市,使超市到三個小區的距離相等,則超市應建在( )
三個居民小區的位置成三角形,現決定在三個小區之間修建一個購物超市,使超市到三個小區的距離相等,則超市應建在( )

A.在∠A、∠B兩內角平分線的交點處
B.在AC、BC兩邊垂直平分線的交點處
C.在AC、BC兩邊高線的交點處
D.在AC、BC兩邊中線的交點處
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】閱讀下列材料:
我們可以通過下列步驟估計![]() 的大小.
的大小.
第一步:因為12=1,22=4,1<2<4,所以1<![]() <2.
<2.
第二步:通過取1和2的平均數縮小![]() 所在的范圍:取
所在的范圍:取![]() ,
,
因為1.52=2.25,2<2.25,所以1<![]() <1.5.
<1.5.
(1)請仿照第一步,通過運算,確定![]() 界于哪兩個相鄰的整數之間?
界于哪兩個相鄰的整數之間?
(2)在1<![]() <1.5的基礎上,重復應用第二步中取平均數的方法,將
<1.5的基礎上,重復應用第二步中取平均數的方法,將![]() 所在的范圍縮小至m<
所在的范圍縮小至m<![]() <n,使得n-m=
<n,使得n-m=![]() .
.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某小型企業實行工資與業績掛鉤制度,工人工資分為A、B、C、D四個檔次.小明對該企業三月份工人工資進行調查,并根據收集到的數據,繪制了如下尚不完整的統計表與扇形統計圖.
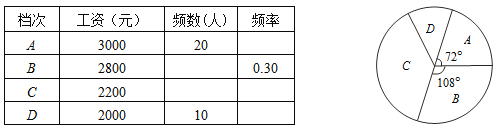
根據上面提供的信息,回答下列問題:
(1)求該企業共有多少人?
(2)請將統計表補充完整;
(3)扇形統計圖中“C檔次”的扇形所對的圓心角是 度.
查看答案和解析>>
科目:初中數學 來源: 題型:
【題目】某校為更好地開展“傳統文化進校園”活動,隨機抽查了部分學生,了解他們最喜愛的傳統文化項目類型(分為書法、圍棋、戲劇、國畫共4類),并將統計結果繪制成如圖不完整的頻數分布表及頻數分布直方圖.
最喜愛的傳統文化項目類型頻數分布表


根據以上信息完成下列問題:
(1)直接寫出頻數分布表中a的值;
(2)補全頻數分布直方圖;
(3)若全校共有學生1500名,估計該校最喜愛圍棋的學生大約有多少人?
查看答案和解析>>
科目:初中數學 來源: 題型:
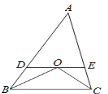
【題目】如圖,在△ABC中,∠B與∠C的平分線交于點O,過點O作DE∥BC,分別交AB,AC于點D,E.若AB=5,AC=4,則△ADE的周長是______
查看答案和解析>>
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com