題目列表(包括答案和解析)
(1)若a.⊥b,求a;
(2)若a∥b,求a.
| axn | xn+1 |
（a為常數(shù)）．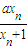
（a為常數(shù)）．
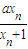（a為常數(shù)）．1．不改變f(x)值域，即不能縮小原函數(shù)定義域。選項(xiàng)B，C，D均縮小了的定義域，故選A。
2．先作出f(x,y)=0關(guān)于軸對稱的函數(shù)的圖象，即為函數(shù)f(-x,y)=0的圖象，又
f(2－x,y)=0即為，即由f(-x,y)=0向右平移2個單位。故選C。
3．命題p為真時，即真數(shù)部分能夠取到大于零的所有實(shí)數(shù)，故二次函數(shù)的判別式，從而；命題q為真時，。
若p或q為真命題，p且q為假命題，故p和q中只有一個是真命題，一個是假命題。
若p為真，q為假時，無解；若p為假，q為真時，結(jié)果為1<a<2，故選C.
4．圖像法解方程，也可代入各區(qū)間的一個數(shù)（特值法或代入法），選C；
5．函數(shù)f(x)的對稱軸為2，結(jié)合其單調(diào)性，選A；
6．從反面考慮，注意應(yīng)用特例，選B；
7．設(shè)tan＝x (x>0），則＋＝，解出x＝2，再用萬能公式，選A；
8．利用是關(guān)于n的一次函數(shù)，設(shè)S＝S＝m，＝x，則（,p）、(,q)、
(x，p+q)在同一直線上，由兩點(diǎn)斜率相等解得x＝0，則答案：0；
9．設(shè)cosx＝t，t∈[-1,1]，則a＝t－t－1∈[－,1]，所以答案：[－,1]；
10．設(shè)高h(yuǎn)，由體積解出h＝2，答案：24；
11．設(shè)長x，則寬，造價y＝4×120＋4x×80＋×80≥1760，答案：1760。
12．運(yùn)用條件知：=2，且
==16
13．依題意可知，從而可知，所以有
，又為正整數(shù)，取，則
，所以，從而，所以，又，所以，因此有最小值為。
下面可證時，，從而，所以, 又,所以,所以,綜上可得:的最小值為11。
14．分析:這是有關(guān)函數(shù)定義域、值域的問題，題目是逆向給出的，解好本題要運(yùn)用復(fù)合函數(shù)，把f(x)分解為u=ax+2x+1和y=lgu 并結(jié)合其圖象性質(zhì)求解．
切實(shí)數(shù)x恒成立． a=0或a＜0不合題意，
解得a＞1．
當(dāng)a＜0時不合題意； a=0時，u=2x+1，u能取遍一切正實(shí)數(shù)；
a＞0時，其判別式Δ=22-4×a×1≥0，解得0＜a≤1．
所以當(dāng)0≤a≤1時f(x)的值域是R．
15．分析：此問題由于常見的思維定勢，易把它看成關(guān)于x的不等式討論。然而，若變換一個角度以m為變量，即關(guān)于m的一次不等式(x－1)m－(2x－1)<0在[-2,2]上恒成立的問題。對此的研究，設(shè)f(m)＝(x－1)m－(2x－1)，則問題轉(zhuǎn)化為求一次函數(shù)（或常數(shù)函數(shù)）f(m)的值在[-2,2]內(nèi)恒為負(fù)值時參數(shù)x應(yīng)該滿足的條件。
解：問題可變成關(guān)于m的一次不等式：(x－1)m－(2x－1)<0在[-2,2] 恒成立，設(shè)f(m)＝(x－1)m－(2x－1), 則
解得x∈（,）
說明 本題的關(guān)鍵是變換角度，以參數(shù)m作為自變量而構(gòu)造函數(shù)式，不等式問題變成函數(shù)在閉區(qū)間上的值域問題。本題有別于關(guān)于x的不等式2x－1>m(x－1)的解集是[-2,2]時求m的值、關(guān)于x的不等式2x－1>m(x－1)在[-2,2]上恒成立時求m的范圍。
一般地，在一個含有多個變量的數(shù)學(xué)問題中，確定合適的變量和參數(shù)，從而揭示函數(shù)關(guān)系，使問題更明朗化。或者含有參數(shù)的函數(shù)中，將函數(shù)自變量作為參數(shù)，而參數(shù)作為函數(shù)，更具有靈活性，從而巧妙地解決有關(guān)問題。
16．分析： ①問利用公式a與S建立不等式，容易求解d的范圍；②問利用S是n的二次函數(shù)，將S中哪一個值最大，變成求二次函數(shù)中n為何值時S取最大值的函數(shù)最值問題。
解：① 由a＝a＋2d＝12,得到a＝12－2d，所以
S＝12a＋66d＝12(12－2d)＋66d＝144＋42d>0，
S＝13a＋78d＝13(12－2d)＋78d＝156＋52d<0。
解得：－<d<－3。
② S＝na＋n(n1－1)d＝n(12－2d)＋n(n－1)d
＝[n－(5－)]－[(5－)]
因?yàn)閐<0，故[n－(5－)]最小時，S最大。由－<d<－3得6<(5－)<6.5，故正整數(shù)n＝6時[n－(5－)]最小，所以S最大。
說明： 數(shù)列的通項(xiàng)公式及前n項(xiàng)和公式實(shí)質(zhì)上是定義在自然數(shù)集上的函數(shù)，因此可利用函數(shù)思想來分析或用函數(shù)方法來解決數(shù)列問題。也可以利用方程的思想，設(shè)出未知的量，建立等式關(guān)系即方程，將問題進(jìn)行算式化，從而簡潔明快。由次可見，利用函數(shù)與方程的思想來解決問題，要求靈活地運(yùn)用、巧妙的結(jié)合，發(fā)展了學(xué)生思維品質(zhì)的深刻性、獨(dú)創(chuàng)性。
本題的另一種思路是尋求a>0、a<0 ，即：由d<0知道a>a>…>a，由S＝13a<0得a<0，由S＝6(a＋a)>0得a>0。所以，在S、S、…、S中，S的值最大。
17．分析：異面直線PB和AC的距離可看成求直線PB上任意一點(diǎn)到AC的距離的最小值，從而設(shè)定變量，建立目標(biāo)函數(shù)而求函數(shù)最小值。
M
A
H
B
D C
解：在PB上任取一點(diǎn)M，作MD⊥AC于D，MH⊥AB于H，
設(shè)MH＝x，則MH⊥平面ABC，AC⊥HD 。
∴MD＝x＋[(2r－x)sinθ]＝(sin＋1)x－4rsinθx＋4rsinθ＝(sinθ＋1)[x－]＋
即當(dāng)x＝時，MD取最小值為兩異面直線的距離。
說明：本題巧在將立體幾何中“異面直線的距離”變成“求異面直線上兩點(diǎn)之間距離的最小值”，并設(shè)立合適的變量將問題變成代數(shù)中的“函數(shù)問題”。一般地，對于求最大值、最小值的實(shí)際問題，先將文字說明轉(zhuǎn)化成數(shù)學(xué)語言后，再建立數(shù)學(xué)模型和函數(shù)關(guān)系式，然后利用函數(shù)性質(zhì)、重要不等式和有關(guān)知識進(jìn)行解答。比如再現(xiàn)性題組第8題就是典型的例子。
18．分析：已知了一個積式，考慮能否由其它已知得到一個和式，再用方程思想求解。
解： 由A、B、C成等差數(shù)列，可得B＝60°；
由△ABC中tanA＋tanB＋tanC＝tanA?tanB?tanC，得
tanA＋tanC＝tanB(tanA?tanC－1)＝ (1＋)
設(shè)tanA、tanC是方程x－(＋3)x＋2＋＝0的兩根，解得x＝1，x＝2＋
設(shè)A<C，則tanA＝1，tanC＝2＋， ∴A＝，C＝
由此容易得到a＝8，b＝4，c＝4＋4。
說明：本題的解答關(guān)鍵是利用“△ABC中tanA＋tanB＋tanC＝tanA?tanB?tanC”這一條性質(zhì)得到tanA＋tanC，從而設(shè)立方程求出tanA和tanC的值，使問題得到解決。
19．分析：當(dāng)x∈(-∞,1]時f(x)＝lg有意義的函數(shù)問題，轉(zhuǎn)化為1＋2＋4a>0在x∈(-∞,1]上恒成立的不等式問題。
解：由題設(shè)可知，不等式1＋2＋4a>0在x∈(-∞,1]上恒成立，
即：()＋()＋a>0在x∈(-∞,1]上恒成立。
設(shè)t＝(), 則t≥， 又設(shè)g(t)＝t＋t＋a，其對稱軸為t＝－
∴ t＋t＋a＝0在[,+∞)上無實(shí)根， 即 g()＝()＋＋a>0，得a>－
所以a的取值范圍是a>－。
說明：對于不等式恒成立，引入新的參數(shù)化簡了不等式后，構(gòu)造二次函數(shù)利用函數(shù)的圖像和單調(diào)性進(jìn)行解決問題，其中也聯(lián)系到了方程無解，體現(xiàn)了方程思想和函數(shù)思想。一般地，我們在解題中要抓住二次函數(shù)及圖像、二次不等式、二次方程三者之間的緊密聯(lián)系，將問題進(jìn)行相互轉(zhuǎn)化。
在解決不等式()＋()＋a>0在x∈(-∞,1]上恒成立的問題時，也可使用“分離參數(shù)法”： 設(shè)t＝(), t≥，則有a＝－t－t∈(－∞,－]，所以a的取值范圍是a>－。其中最后得到a的范圍，是利用了二次函數(shù)在某區(qū)間上值域的研究，也可屬應(yīng)用“函數(shù)思想”。
20．解：f(x)=cosqsinx－(sinxcosq－cosxsinq)+(tanq－2)sinx－sinq
=sinqcosx+(tanq－2)sinx－sinq
因?yàn)?i>f(x)是偶函數(shù)，
所以對任意xÎR，都有f(－x)=f(x)，
即sinqcos(－x)+(tanq－2)sin(－x)－sinq=sinqcosx+(tanq－2)sinx－sinq,
即(tanq－2)sinx=0，
所以tanq=2
由
解得或
此時，f(x)=sinq(cosx－1).
當(dāng)sinq=時，f(x)=(cosx－1)最大值為0，不合題意最小值為0，舍去；
當(dāng)sinq=時，f(x)=(cosx－1)最小值為0，
當(dāng)cosx=－1時，f(x)有最大值為,
自變量x的集合為{x|x=2kp+p,kÎZ}．
21．解：（1）；．，
若上是增函數(shù)，則恒成立，即
若上是減函數(shù)，則恒成立，這樣的不存在．
綜上可得：．
（2）（證法一）設(shè)，由得，于是有，（1）－（2）得：，化簡可得
，，，故，即有．
（證法二）假設(shè)，不妨設(shè)，由（1）可知在
上單調(diào)遞增，故，
這與已知矛盾，故原假設(shè)不成立，即有．
國際學(xué)校優(yōu)選 - 練習(xí)冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權(quán)舉報專區(qū)
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com