
題目列表(包括答案和解析)
| 1 |
| x |
| an-1 |
| 1 |
| an |
| k |
| 3 |
| 3n-8k |
| k |
| x2 |
| a2 |
| y2 |
| b2 |
| 2 |
 (a>b>0),橢圓的左右焦點(diǎn)分別為F1、F2,若三角形PF1F2的面積為2,且a2,b2的等比中項(xiàng)為6
(a>b>0),橢圓的左右焦點(diǎn)分別為F1、F2,若三角形PF1F2的面積為2,且a2,b2的等比中項(xiàng)為6 .
.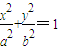 (a>b>0),橢圓的左右焦點(diǎn)分別為F1、F2,若三角形PF1F2的面積為2,且a2,b2的等比中項(xiàng)為6
(a>b>0),橢圓的左右焦點(diǎn)分別為F1、F2,若三角形PF1F2的面積為2,且a2,b2的等比中項(xiàng)為6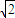 .
.已知點(diǎn)P在曲線C:y=![]() (x>1)上,設(shè)曲線C在點(diǎn)P處的切線為l,若l與函數(shù)y=kx(k>0)的圖像交于點(diǎn)A,與x軸交于點(diǎn)B,設(shè)點(diǎn)P的橫坐標(biāo)為t,設(shè)A、B的橫坐標(biāo)分別為xA、xB,記f(t)=xA·xB.
(x>1)上,設(shè)曲線C在點(diǎn)P處的切線為l,若l與函數(shù)y=kx(k>0)的圖像交于點(diǎn)A,與x軸交于點(diǎn)B,設(shè)點(diǎn)P的橫坐標(biāo)為t,設(shè)A、B的橫坐標(biāo)分別為xA、xB,記f(t)=xA·xB.
(Ⅰ)求f(t)的解析式;
(Ⅱ)設(shè)數(shù)列{an}(n≥1,n∈N)滿足a1=1,an=f(![]() )(n≥2),數(shù)列{bn}(n≥1,n∈N)滿足bn=
)(n≥2),數(shù)列{bn}(n≥1,n∈N)滿足bn=![]() ,求{an}和{bn}的通項(xiàng)公式;
,求{an}和{bn}的通項(xiàng)公式;
(Ⅲ)在(Ⅱ)的條件下,當(dāng)1<k<3時(shí),證明不等式:a1+a2+a3+…+an>![]() .
.
一、選擇題:
題號(hào)
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
A
D
A
B
D
B
C
B
C
D
B
1.提示:學(xué)(五).files/image234.gif)
學(xué)(五).files/image236.gif) ,故選C。
,故選C。
2.提示:“任意的”否定為“存在”;“>”的否定為“學(xué)(五).files/image238.gif) ”,故選A
”,故選A
3.提示:學(xué)(五).files/image240.gif) 又
又學(xué)(五).files/image242.gif) ,所以
,所以學(xué)(五).files/image244.gif) ,故選D。
,故選D。
4.提示:在AB上取點(diǎn)D,使得學(xué)(五).files/image246.gif) ,則點(diǎn)P只能在AD內(nèi)運(yùn)動(dòng),則
,則點(diǎn)P只能在AD內(nèi)運(yùn)動(dòng),則學(xué)(五).files/image248.gif) ,
,
5.提示:排除法選B。
6.提示:由圖(1)改為圖(2)后每次循環(huán)時(shí)學(xué)(五).files/image250.gif) 的值都為1,因此運(yùn)行過(guò)程出現(xiàn)無(wú)限循環(huán),故選D
的值都為1,因此運(yùn)行過(guò)程出現(xiàn)無(wú)限循環(huán),故選D
7.提示:由莖葉圖的定義,甲得分為7,8,9,15,19,23,24,26,32,41。共11個(gè)數(shù),19是中位數(shù),乙得分為5,7,11,11,13,20,22,30,31,40。共11個(gè)數(shù),13是中位數(shù)。
故選B。
8.提示:學(xué)(五).files/image252.gif) 得
得學(xué)(五).files/image254.gif) 所以
所以學(xué)(五).files/image256.gif) ,故選C。
,故選C。
學(xué)(五).files/image257.gif) 9.提示:由
9.提示:由學(xué)(五).files/image259.gif) 及
及學(xué)(五).files/image261.gif) 得
得
學(xué)(五).files/image263.gif) 如圖
如圖
過(guò)A作學(xué)(五).files/image265.gif) 于M,則
于M,則
學(xué)(五).files/image267.gif)
學(xué)(五).files/image269.gif)
學(xué)(五).files/image271.gif)
學(xué)(五).files/image273.gif) 得
得學(xué)(五).files/image275.gif) .
.
故選B.
10.提示:不妨設(shè)點(diǎn)(2,0)與曲線學(xué)(五).files/image067.gif) 上不同的三的點(diǎn)距離為分別
上不同的三的點(diǎn)距離為分別學(xué)(五).files/image277.gif) ,它們組成的等比數(shù)列的公比為
,它們組成的等比數(shù)列的公比為學(xué)(五).files/image279.gif) 若令
若令學(xué)(五).files/image281.gif) ,顯然
,顯然學(xué)(五).files/image283.gif) ,又
,又學(xué)(五).files/image285.gif) 所以
所以學(xué)(五).files/image287.gif) ,
,學(xué)(五).files/image289.gif) 不能取到
不能取到學(xué)(五).files/image036.gif) 。故選B。
。故選B。
11.提示:使用特值法:取集合學(xué)(五).files/image292.gif) 當(dāng)
當(dāng)學(xué)(五).files/image294.gif) 可以排除A、B;
可以排除A、B;
取集合學(xué)(五).files/image296.gif) ,當(dāng)
,當(dāng)學(xué)(五).files/image298.gif) 可以排除C;故選D;
可以排除C;故選D;
12.提示:n棱柱有學(xué)(五).files/image300.gif) 個(gè)頂點(diǎn),被平面截去一個(gè)三棱錐后,可以分以下6種情形(圖1~6)
個(gè)頂點(diǎn),被平面截去一個(gè)三棱錐后,可以分以下6種情形(圖1~6)
學(xué)(五).files/image302.gif)
學(xué)(五).files/image303.gif)
學(xué)(五).files/image304.gif)
學(xué)(五).files/image305.gif)
學(xué)(五).files/image306.gif)
學(xué)(五).files/image307.gif)
2在圖4,圖6所示的情形,還剩學(xué)(五).files/image300.gif) 個(gè)頂點(diǎn);
個(gè)頂點(diǎn);
在圖5的情形,還剩學(xué)(五).files/image309.gif) 個(gè)頂點(diǎn);
個(gè)頂點(diǎn);
在圖2,圖3的情形,還剩學(xué)(五).files/image311.gif) 個(gè)頂點(diǎn);
個(gè)頂點(diǎn);
在圖1的情形,還剩下學(xué)(五).files/image313.gif) 個(gè)頂點(diǎn).故選B.
個(gè)頂點(diǎn).故選B. 學(xué)(五).files/image315.jpg)
二、填空題:
13.4
提示:學(xué)(五).files/image317.gif)
學(xué)(五).files/image319.gif) 由(1),(2)得
由(1),(2)得學(xué)(五).files/image321.gif) 或
或學(xué)(五).files/image323.gif) ,所以
,所以學(xué)(五).files/image325.gif) 。
。
14.學(xué)(五).files/image327.gif)
提示:斜率學(xué)(五).files/image329.gif) ,切點(diǎn)
,切點(diǎn)學(xué)(五).files/image331.gif) ,所以切線方程為:
,所以切線方程為:學(xué)(五).files/image333.gif)
15.學(xué)(五).files/image335.gif)
提示:當(dāng)學(xué)(五).files/image337.gif) 時(shí),不等式無(wú)解,當(dāng)
時(shí),不等式無(wú)解,當(dāng)學(xué)(五).files/image339.gif) 時(shí),不等式變?yōu)?sub>
時(shí),不等式變?yōu)?sub>學(xué)(五).files/image341.gif) ,
,
由題意得學(xué)(五).files/image343.gif) 或
或學(xué)(五).files/image345.gif) ,所以,
,所以,學(xué)(五).files/image347.gif) 或
或學(xué)(五).files/image349.gif)
16.學(xué)(五).files/image351.gif)
三、解答題:
17.解:① ∵學(xué)(五).files/image353.gif) ∴
∴學(xué)(五).files/image355.gif) 的定義域?yàn)镽;
的定義域?yàn)镽;
② ∵學(xué)(五).files/image357.gif) ,
,
∴學(xué)(五).files/image178.gif) 為偶函數(shù);
為偶函數(shù);
③ ∵學(xué)(五).files/image360.gif) , ∴
, ∴學(xué)(五).files/image178.gif) 是周期為
是周期為學(xué)(五).files/image363.gif) 的周期函數(shù);
的周期函數(shù);
④ 當(dāng)學(xué)(五).files/image365.gif) 時(shí),
時(shí),學(xué)(五).files/image178.gif) =
=學(xué)(五).files/image367.gif) ,
,
∴當(dāng)學(xué)(五).files/image365.gif) 時(shí)
時(shí)學(xué)(五).files/image178.gif) 單調(diào)遞減;當(dāng)
單調(diào)遞減;當(dāng)學(xué)(五).files/image371.gif) 時(shí),
時(shí),
學(xué)(五).files/image178.gif) =
=學(xué)(五).files/image373.gif) ,
,
學(xué)(五).files/image178.gif) 單調(diào)遞增;又∵
單調(diào)遞增;又∵學(xué)(五).files/image178.gif) 是周期為
是周期為學(xué)(五).files/image363.gif) 的偶函數(shù),∴
的偶函數(shù),∴學(xué)(五).files/image178.gif) 在
在學(xué)(五).files/image378.gif) 上單調(diào)遞增,在
上單調(diào)遞增,在學(xué)(五).files/image380.gif) 上單調(diào)遞減(
上單調(diào)遞減(學(xué)(五).files/image382.gif) );
);
⑤ ∵當(dāng)學(xué)(五).files/image384.gif) 時(shí)
時(shí)學(xué)(五).files/image386.gif) ;
;
當(dāng)學(xué)(五).files/image387.gif) 時(shí)
時(shí)學(xué)(五).files/image389.gif) .∴
.∴學(xué)(五).files/image178.gif) 的值域?yàn)?sub>
的值域?yàn)?sub>學(xué)(五).files/image392.gif) ;
;
⑥由以上性質(zhì)可得:學(xué)(五).files/image178.gif) 在
在學(xué)(五).files/image395.gif) 上的圖象如圖所示:
上的圖象如圖所示:
學(xué)(五).files/image397.jpg)
18.解:(Ⅰ)取PC的中點(diǎn)G,連結(jié)EG,GD,則學(xué)(五).files/image399.gif)
由(Ⅰ)知FD⊥平面PDC,學(xué)(五).files/image401.gif) 面PDC,所以FD⊥DG。
面PDC,所以FD⊥DG。
所以四邊形FEGD為矩形,因?yàn)镚為等腰Rt△RPD斜邊PC的中點(diǎn),
所以DG⊥PC,