
題目列表(包括答案和解析)
已知數列 滿足
滿足 (I)求數列
(I)求數列 的通項公式;
的通項公式;
(II)若數列 中
中 ,前
,前 項和為
項和為 ,且
,且 證明:
證明:
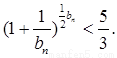
【解析】第一問中,利用 ,
,
∴數列{ }是以首項a1+1,公比為2的等比數列,即
}是以首項a1+1,公比為2的等比數列,即
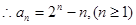
第二問中,

進一步得到得 即
即
即 是等差數列.
是等差數列.
然后結合公式求解。
解:(I) 解法二、 ,
,
∴數列{ }是以首項a1+1,公比為2的等比數列,即
}是以首項a1+1,公比為2的等比數列,即
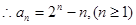
(II)
 ………②
………②
由②可得: …………③
…………③
③-②,得 即
即 …………④
…………④
又由④可得 …………⑤
…………⑤
⑤-④得
即 是等差數列.
是等差數列.


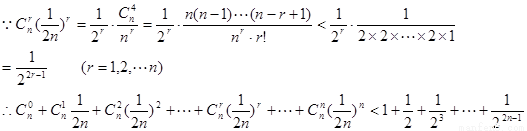


(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(理)對于數列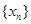 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數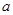 ,公比為正整數
,公比為正整數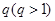 的無窮等比數列
的無窮等比數列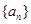 的子數列問題. 為此,他任取了其中三項
的子數列問題. 為此,他任取了其中三項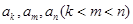 .
.
(1) 若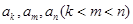 成等比數列,求
成等比數列,求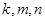 之間滿足的等量關系;
之間滿足的等量關系;
(2) 他猜想:“在上述數列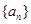 中存在一個子數列
中存在一個子數列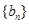 是等差數列”,為此,他研究了
是等差數列”,為此,他研究了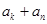 與
與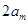 的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確;
的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確;
(3) 他又想:在首項為正整數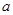 ,公差為正整數
,公差為正整數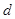 的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.
的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.
(本題滿分18分) 本題共有3個小題,第1小題滿分4分,第2小題滿分6分. 第3小題滿分8分.
(理)對于數列 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數 ,公比為正整數
,公比為正整數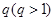 的無窮等比數列
的無窮等比數列 的子數列問題. 為此,他任取了其中三項
的子數列問題. 為此,他任取了其中三項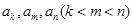 .
.
(1) 若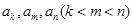 成等比數列,求
成等比數列,求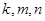 之間滿足的等量關系;
之間滿足的等量關系;
(2) 他猜想:“在上述數列 中存在一個子數列
中存在一個子數列 是等差數列”,為此,他研究了
是等差數列”,為此,他研究了 與
與 的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確;
的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確;
(3) 他又想:在首項為正整數 ,公差為正整數
,公差為正整數 的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.
的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.
 ,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數
,從中選取若干項,不改變它們在原來數列中的先后次序,得到的數列稱為是原來數列的一個子數列. 某同學在學習了這一個概念之后,打算研究首項為正整數 ,公比為正整數
,公比為正整數 的無窮等比數列
的無窮等比數列 的子數列問題. 為此,他任取了其中三項
的子數列問題. 為此,他任取了其中三項 .
. 成等比數列,求
成等比數列,求 之間滿足的等量關系;
之間滿足的等量關系; 中存在一個子數列
中存在一個子數列 是等差數列”,為此,他研究了
是等差數列”,為此,他研究了 與
與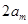 的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確;
的大小關系,請你根據該同學的研究結果來判斷上述猜想是否正確; ,公差為正整數
,公差為正整數 的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.
的無窮等差數列中是否存在成等比數列的子數列?請你就此問題寫出一個正確命題,并加以證明.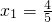 ,
,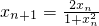 ;對函數f(x)在(-2,2)上有意義,
;對函數f(x)在(-2,2)上有意義,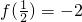 ,且滿足x,y∈(-2,2)時,有
,且滿足x,y∈(-2,2)時,有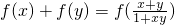 成立,則數列{f(xn)}是
成立,則數列{f(xn)}是湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com