精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

已知等差數(shù)列{a_n}的首項(xiàng)為4，公差為4，其前n項(xiàng)和為S_n，則數(shù)列 {}的前n項(xiàng)和為（　　）

A．

B．

C．

D．

考點(diǎn)：	數(shù)列的求和；等差數(shù)列的性質(zhì)．
專題：	等差數(shù)列與等比數(shù)列．
分析：	利用等差數(shù)列的前n項(xiàng)和即可得出Sn，再利用“裂項(xiàng)求和”即可得出數(shù)列 {}的前n項(xiàng)和．
解答：	解：∵Sn=4n+=2n2+2n， ∴． ∴數(shù)列 {}的前n項(xiàng)和===． 故選A．
點(diǎn)評：	熟練掌握等差數(shù)列的前n項(xiàng)和公式、“裂項(xiàng)求和”是解題的關(guān)鍵．

在等差數(shù)列{a_n}中，a₁=3，其前n項(xiàng)和為S_n，等比數(shù)列{b_n}的各項(xiàng)均為正數(shù)，b₁=1，公比為q,且b₂+ S₂=12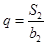，.（Ⅰ）求a_n 與b_n；（Ⅱ）設(shè)數(shù)列{c_n}滿足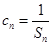，求{c_n}的前n項(xiàng)和T_n.

【解析】本試題主要是考查了等比數(shù)列的通項(xiàng)公式和求和的運(yùn)用。第一問中，利用等比數(shù)列{b_n}的各項(xiàng)均為正數(shù)，b₁=1，公比為q,且b₂+ S₂=12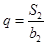，，可得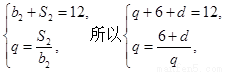，解得q=3或q=-4(舍),d=3.得到通項(xiàng)公式故a_n=3+3(n-1)=3n, b_n=3 ^n-1.     第二問中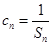，，由第一問中知道，然后利用裂項(xiàng)求和得到T_n.

解： (Ⅰ) 設(shè)：{a_n}的公差為d,

因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921190757897157/SYS201206192120143914538050_ST.files/image003.png">解得q=3或q=-4(舍),d=3.

故a_n=3+3(n-1)=3n, b_n=3 ^n-1.                       ………6分

(Ⅱ)因?yàn)?img src="http://thumb.zyjl.cn/pic6/res/gzsx/web/STSource/2012061921190757897157/SYS201206192120143914538050_ST.files/image004.png">……………8分

 

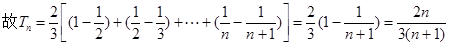
設(shè)數(shù)列的前n項(xiàng)和為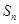，點(diǎn)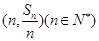均在函數(shù)y＝－x+12的圖像上.

（Ⅰ）寫出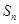關(guān)于n的函數(shù)表達(dá)式；

（Ⅱ）求證：數(shù)列是等差數(shù)列；

（Ⅲ）求數(shù)列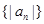的前n項(xiàng)的和.                               

【解析】本試題主要是考查了數(shù)列的概念和數(shù)列的求和的綜合運(yùn)用。

 

已知數(shù)列中，，，數(shù)列中，，且點(diǎn)在直線上。

（1）求數(shù)列的通項(xiàng)公式；

（2）求數(shù)列的前項(xiàng)和；

（3）若，求數(shù)列的前項(xiàng)和；

【解析】第一問中利用數(shù)列的遞推關(guān)系式

，因此得到數(shù)列的通項(xiàng)公式；

第二問中，在 即為：

即數(shù)列是以的等差數(shù)列

得到其前n項(xiàng)和。

第三問中， 又   

，利用錯(cuò)位相減法得到。

解：（1）

  即數(shù)列是以為首項(xiàng)，2為公比的等比數(shù)列

                  ……4分

（2）在 即為：

即數(shù)列是以的等差數(shù)列

         ……8分

（3） 又   

   ①         ②

①-  ②得到

  

 

已知正項(xiàng)數(shù)列的前n項(xiàng)和滿足：，

（1）求數(shù)列的通項(xiàng)和前n項(xiàng)和；

（2）求數(shù)列的前n項(xiàng)和；

（3）證明：不等式  對任意的，都成立．

【解析】第一問中，由于所以

兩式作差，然后得到

從而得到結(jié)論

第二問中，利用裂項(xiàng)求和的思想得到結(jié)論。

第三問中，

又

       

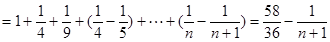
結(jié)合放縮法得到。

解：（1）∵     ∴

      ∴

      ∴   ∴  ………2分

      又∵正項(xiàng)數(shù)列，∴           ∴ 

又n=1時(shí)，

∴   ∴數(shù)列是以1為首項(xiàng)，2為公差的等差數(shù)列……………3分

∴                             …………………4分

∴                   …………………5分 

（2）       …………………6分

    ∴

                          …………………9分

（3）

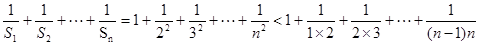
      …………………12分

又

        ，

   ∴不等式  對任意的，都成立．