
題目列表(包括答案和解析)
|
| x2 |
| 4 |
| y2 |
| 3 |
| π |
| 6 |
| 3 |
B.選修4-2:矩陣與變換
已知矩陣A ,其中
,其中 ,若點
,若點 在矩陣A的變換下得到
在矩陣A的變換下得到 .
.
(1)求實數(shù) 的值;
的值;
(2)矩陣A的特征值和特征向量.
B.選修4—2 矩陣與變換
已知矩陣
 ,其中
,其中 ,若點
,若點 在矩陣
在矩陣 的變換下得到點
的變換下得到點 ,
,
(1)求實數(shù)a的值;
(2)求矩陣 的特征值及其對應的特征向量.
的特征值及其對應的特征向量.
(21分).若非零函數(shù)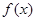 對任意實數(shù)
對任意實數(shù)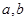 均有¦(a+b)=¦(a)·¦(b),且當
均有¦(a+b)=¦(a)·¦(b),且當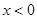 時,
時,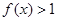 .
.
(1)求證: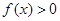 ;
;
(2)求證: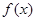 為減函數(shù);
為減函數(shù);
(3)當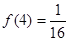 時,解不等式
時,解不等式
B.選修4-2:矩陣與變換
已知矩陣A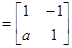 ,其中
,其中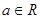 ,若點
,若點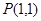 在矩陣A的變換下得到
在矩陣A的變換下得到 .
.
(1)求實數(shù)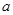 的值;
的值;
(2)矩陣A的特征值和特征向量.
一、填空題:(5’×11=55’)
題號
1
2
3
4
5
6
答案
2008學年度高三第一學期質(zhì)量調(diào)研測試(數(shù)學文).files/image190.gif)
2008學年度高三第一學期質(zhì)量調(diào)研測試(數(shù)學文).files/image192.gif)
0
(1,2)
2
2008學年度高三第一學期質(zhì)量調(diào)研測試(數(shù)學文).files/image194.gif)
題號
7
8
9
10
11
答案
2008學年度高三第一學期質(zhì)量調(diào)研測試(數(shù)學文).files/image196.gif)
4
8.3
2008學年度高三第一學期質(zhì)量調(diào)研測試(數(shù)學文).files/image198.gif)
②、③
二、選擇題:(4’×4=16’)
題號
12
13
14
15
答案
A
C
B
|