題目列表(包括答案和解析)
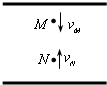如圖所示，帶等量異種電荷的兩平行金屬板在真空中水平放置，M、N為板間同一電場線上的兩點，一帶電粒子（不計重力）以速度vM經過M點所在電場線上向下運動，且未與下板接觸，一段時間后，粒子以速度vN折回N點．則（ ）| A、粒子受電場力的方向一定由M指向N | B、粒子在M點的加速度一定比在N點的大 | C、粒子在M點的電勢能一定比在N點的小 | D、電場中M點的電勢一定高于N點的電勢 |
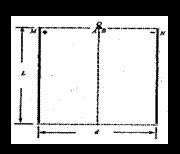如圖所示，帶等量異種電荷的兩平行金屬板豎直放置（M板帶正電，N板帶負電），板間距為d=80cm，板長為L，板間電壓為U=100V。兩極板上邊緣連線的中點處有一用水平輕質絕緣細線拴接的完全相同的小球A和B組成的裝置Q，Q處于靜止狀態，該裝置中兩球之間有一處于壓縮狀態的絕緣輕質小彈簧（球與彈簧不拴接），左邊A球帶正電，電荷量為q=4×10-5C，右邊B球不帶電，兩球質量均為m=1.0×10-3kg.某時刻,裝置Q中細線突然斷裂,A、B兩球立即同時獲得大小相等、方向相反的速度（彈簧恢復原長）。若A、B之間彈簧被壓縮時所具有的彈性能為1.0×10-3J，小球A、B均可視為質點，Q裝置中彈簧的長度不計，小球帶電不影響板章勻強電場，不計空氣阻力，取g=10m/s2。求：
（1）為使小球不與金屬板相碰，金屬板長度L應滿足什么條件？
（2）當小球B飛離電場恰好不與金屬板相碰時，小球A飛離電場時的動能是多大？
（3）從兩小球彈開進入電場開始，到兩小球間水平距離為30cm時，小球A的電勢能增加了多少？
（12分）如圖所示，帶等量異種電荷的兩平行金屬板豎直放置（M板帶正電，N板帶負電），板間距為d=80cm，板長為L，板間電壓為U=100V。兩極板上邊緣連線的中點處有一用水平輕質絕緣細線拴接的完全相同的小球A和B組成的裝置Q，在外力作用下Q處于靜止狀態，該裝置中兩球之間有一處于壓縮狀態的絕緣輕質小彈簧（球與彈簧不拴接），左邊A球帶正電，電荷量為q=4×10-5C，右邊B球不帶電，兩球質量均為m=1.0×10-3kg，某時刻裝置Q中細線突然斷裂,A、B兩球立即同時獲得大小相等、方向相反的速度（彈簧恢復原長）。若A、B之間彈簧被壓縮時所具有的彈性能為1.0×10-3J，小球A、B均可視為質點，Q裝置中彈簧的長度不計，小球帶電不影響板間勻強電場，不計空氣阻力，取g=10m/s2。求：
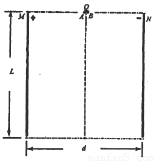
（1）為使小球不與金屬板相碰，金屬板長度L應滿足什么條件？
（2）當小球B飛離電場恰好不與金屬板相碰時，小球A飛離電場時的動能是多大？
（3）從兩小球彈開進入電場開始，到兩小球間水平距離為30cm時，小球A的電勢能增加了多少？
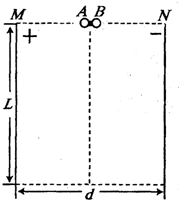
（12分）如圖所示，帶等量異種電荷的兩平行金屬板豎直放置（M板帶正電，N板帶負電），板間距為d=80cm，板長為L，板間電壓為U=100V。兩極板上邊緣連線的中點處有一用水平輕質絕緣細線拴接的完全相同的小球A和B組成的裝置Q，在外力作用下Q處于靜止狀態，該裝置中兩球之間有一處于壓縮狀態的絕緣輕質小彈簧（球與彈簧不拴接），左邊A球帶正電，電荷量為q=4×10-5C，右邊B球不帶電，兩球質量均為m=1.0×10-3kg，某時刻裝置Q中細線突然斷裂,A、B兩球立即同時獲得大小相等、方向相反的速度（彈簧恢復原長）。若A、B之間彈簧被壓縮時所具有的彈性能為1.0×10-3J，小球A、B均可視為質點，Q裝置中彈簧的長度不計，小球帶電不影響板間勻強電場，不計空氣阻力，取g=10m/s2。求：
（1）為使小球不與金屬板相碰，金屬板長度L應滿足什么條件？
（2）當小球B飛離電場恰好不與金屬板相碰時，小球A飛離電場時的動能是多大？
（3）從兩小球彈開進入電場開始，到兩小球間水平距離為30cm時，小球A的電勢能增加了多少？
一．單項選擇題： 1.B 2.D 3.C 4.C 5.A
二．不定項選擇題：6.BC 7.AB 8.ABC 9.AC
三．簡答題
10.（1）將樣品水平放置在光滑水平面上，用滑輪將豎直向下的力變為水平的拉力。（2分）
（2）
（3）①F＝2×106X（N） （3分）
②平方的倒數（2分）、的大小 （2分）
11．（1）刻度尺 交流 （2）D （3）B（4）GK（學生只要取勻速部分均為正確）（各3分）
四．論述、計算題：
12. 解：（1）女運動員做圓周運動的角速度即男運動員轉動的角速度。則
（2分） 由 
得：
（3分）
（2）由
（2分） 解得：
（
均給分）（3分）
13. 解：⑴根據萬有引力定律和向心力公式：
G
（2分） g = G
（2分） 解之得：r =
（2分）
⑵設月球表面處的重力加速度為g月，根據題意：
t =
（2分） g月 = G
（2分） 解之得：
（2分）
14. 解：（1）根據牛頓第二定律，滑塊相對車滑動時的加速度
（1分）
滑塊相對車滑動的時間 
（1分）
滑塊相對車滑動的距離 
（1分）
滑塊與車摩擦產生的內能 
（1分）
由上述各式解得 
（與動摩擦因數μ無關的定值）
（1分）
（2）設恒力F取最小值為F1，滑塊加速度為a1，此時滑塊恰好到達車的左端，則
滑塊運動到車左端的時間 
（1分）
由幾何關系有 
（1分）
由牛頓定律有 
（2分）
代入數據解得 
（2分）
則恒力F大小應該滿足條件是 
（1分）
15. 解：（1）建立如圖所示的直角坐標系。
又機械能守恒定律
得小球彈開時獲得的初速度
m/s
（1分）
進入電場，A球水平方向做勻減速運動，B球水平方向做勻速運動，故B碰不到極板，A球碰不到極板。B球進入電場后向右做平拋運動，平拋時間
s
（1分）
0.4s內的豎直位移
m
（1分）
即，為使小球不與金屬板相撞，金屬板長度L<0.8m （1分）
（2）水平方向上，A球向左做勻減速運動，其加速度
m/s2，方向向右
（1分）
當小球B恰不與金屬板相撞時，A球飛離電場時沿水平方向的位移
（2分）
由功能關系得A球離開電場時的動能
J
（2分）
（3）兩小球進入電場后，豎直方向均做自由落體運動，加速度為g，因此，A、B兩小球在運動過程中始終位于同一條直線上。
當兩小球間的距離為s=30cm時
解得
（舍去） （2分）
此時A球水平位移為
（2分）
小球A的電勢能增加量為
（2分）
16.解：(1) A物體沿斜面下滑時有
∴
m/s2
（1分）
B物體沿斜面下滑時有
∴
（1分）
分析可知，撤去固定A、B的外力后，物體B恰好靜止于斜面上，物體A將沿斜面向下做勻加速直線運動． （1分）
A與B第一次碰撞前的速度
B的速率為零 （1分）
(2)從AB開始運動到第一次碰撞用時
（1分）
兩物體相碰后，A物體的速度變為零，以后再做勻加速運動，而B物體將以
的速度沿斜面向下做勻速直線運動．
（1分）
設再經t2時間相碰，則有
（1分）
解之可得t2=0.8s （1分）
故從A開始運動到兩物體第二次相碰，共經歷時間
t=t1+t2=0.4+0.8=1.2s （1分）
（3）從第2次碰撞開始，每次A物體運動到與B物體碰撞時，速度增加量均為Δv=at2=2.5×0.8m/s=2m/s，由于碰后速度交換，因而碰后B物體的速度為：
第一次碰后： vB1=1m/s
第二次碰后： vB2=2m/s
第三次碰后： vB3=3m/s……
第n次碰后： vBn=nm/s
每段時間內，B物體都做勻速直線運動，則第n次碰前所運動的距離為
sB=[1+2+3+……+（n-1）]×t2=
m (n=1，2，3，…，n-1) （3分）
A物體比B物體多運動L長度，則
sA = L+sB=[0.2+]m
（2分）
則
J （1分）
J
（1分）
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com