題目列表(包括答案和解析)
設函數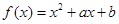
。若
，則
的最大值為
A． | B．6 | C．7 | D．10 |
。若
，則
的最大值為A． | B．6 | C．7 | D．10 |
．設函數f（x）= 
x2＋bx＋1（，b∈R）
（1）若f（－1）=0，則對任意實數均有f（x）≥0成立，求f（x）的表達式；
（2）在（1）的條件下，當x∈[－2，2]時，g（x）= f（x）－kx是單調函數，求實數k的取值范圍。
設函數
在
內有定義.對于給定的正數K，定義函數 
取函數
。若對任意的
，恒有
，則( )
A．K的最大值為2 B．K的最小值為2
C．K的最大值為1 D．K的最小值為1
設函數
的定義域為
，若存在常數
，使
對一切實數
均成立，則稱為
函數．給出下列函數：
①
；②
；③
；④
；⑤是定義在上的奇函數，且滿足對一切實數
、
均有
．其中是函數的序號為 。
一、選擇題 CAADD ABDAB CB
二、填空題 
．
．
．
．
三、解答題
．
的周期為
，最大值為
．
令
，
得
，
．
∴的單調減區間為
．
．事件
，
表示甲以
獲勝；
表示乙以獲勝，、互斥，
∴
．
事件
，
表示甲以
獲勝；
表示甲以獲勝， 、互斥，
∴
延長
、
交于
，則
．
連結
，并延長交
延長線于
，則
，
，
在
中，
為中位線，
，
又
，
∴
．
∵
中，
，
∴
．
即
，又
，
，
∴
，∴
，
∴
為平面
與平面
所成二面角的平面角。
又
，
∴所求二面角大小為
．
．由
，
，
知
，
，同理
，
．
又
，
∴
構成以
為首項，以為公比的等比數列。
∴
，即
．
．
．
，且
的圖象經過點
和
，
∴，
為
的兩根．
∴
∴
由
解
得
∴
要使對
，不等式
恒成立，
只需
即可．
∵
，
∴在
上單調遞減，在
上單調遞增，在
上單調遞減．
又
，
，
∴
，
∴
，
解得
，即為
的取值范圍．
．由題意知，橢圓
的焦點
，
，頂點
，
，
∴雙曲線
中
，
，
．
∴的方程為：
．
聯立
，得
，
∴
且
，
設
，
，
則
，
∴
．
又
，即
，
∴
，
即
．
∴
，
，
由①②得
的范圍為
．
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話：027-86699610 舉報郵箱：58377363@163.com