
題目列表(包括答案和解析)
已知函數(shù)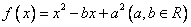
(1)若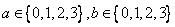 ,求方程
,求方程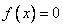 有實(shí)數(shù)根的概率;
有實(shí)數(shù)根的概率;
(2)若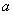 從區(qū)間
從區(qū)間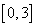 內(nèi)任取一個(gè)數(shù),
內(nèi)任取一個(gè)數(shù),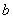 從區(qū)間
從區(qū)間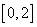 內(nèi)任取一個(gè)數(shù),求方程
內(nèi)任取一個(gè)數(shù),求方程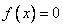 有實(shí)數(shù)根的概率。
有實(shí)數(shù)根的概率。
已知關(guān)于x的方程x2+2ax+b=0,其中,![]() ,b∈[0,2].
,b∈[0,2].
(1)求方程有實(shí)根的概率;
(2)若a∈Z,b∈Z,求方程有實(shí)根的概率.
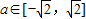 ,b∈[0,2].
,b∈[0,2].| 2 |
| 2 |
已知函數(shù)![]() (
(![]()
![]() ).
).
(1) 若![]() ∈{0,1,2,3},b∈{0,1,2,3},求方程
∈{0,1,2,3},b∈{0,1,2,3},求方程![]() 有實(shí)數(shù)根的概率;
有實(shí)數(shù)根的概率;
(2) 若![]() 從區(qū)間
從區(qū)間![]() 內(nèi)任取一個(gè)數(shù),
內(nèi)任取一個(gè)數(shù),![]() 從區(qū)間
從區(qū)間![]() 內(nèi)任取一個(gè)數(shù),求方程
內(nèi)任取一個(gè)數(shù),求方程![]() 有實(shí)數(shù)根的概率.
有實(shí)數(shù)根的概率.
一、填空題
1.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image215.gif) ; 2.
; 2.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image217.gif) ;3.
;3.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image219.gif) ; 4.
; 4.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image221.gif) ;5. 11; 6.210; 7.16;
8.③; 9.
;5. 11; 6.210; 7.16;
8.③; 9.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image223.gif) ; 10.
; 10.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image225.gif) ; 11.
; 11.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image227.gif) ; 12.
; 12.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image229.gif) ; 13.
; 13.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image231.gif) ; 14.
; 14.年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image233.gif) (結(jié)果為
(結(jié)果為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image235.gif) 不扣分).
不扣分).
二、解答題
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image237.jpg) 15.(本小題滿分14分)
15.(本小題滿分14分)
解:(1)50;0.04;0.10. ………… 6分
(2)如圖. ……………… 10分
(3)在隨機(jī)抽取的年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image239.gif) 名同學(xué)中有
名同學(xué)中有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image241.gif) 名
名
出線,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image243.gif) . ………… 13分
. ………… 13分
答:在參加的年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image245.gif) 名中大概有63名同學(xué)出線.
名中大概有63名同學(xué)出線.
………………… 14分
16.(本小題滿分14分)
解:年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image127.gif) 真,則有
真,則有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image248.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image250.gif) . ------------------4分
. ------------------4分
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image131.gif) 真,則有
真,則有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image253.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image255.gif) . ----------------9分
. ----------------9分
若年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image127.gif) 、
、年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image131.gif) 中有且只有一個(gè)為真命題,則
中有且只有一個(gè)為真命題,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image127.gif) 、
、年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image131.gif) 一真一假.
一真一假.
①若年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image127.gif) 真、
真、年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image131.gif) 假,則
假,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image250.gif) ,且
,且年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image257.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image259.gif) ≤
≤年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image261.gif) ; ----------------11分
; ----------------11分
②若年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image127.gif) 假、
假、年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image131.gif) 真,則
真,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image263.gif) ,且
,且年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image255.gif) ,即3≤
,即3≤年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image265.gif) . ----------------13分
. ----------------13分
故所求范圍為:年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image259.gif) ≤
≤年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image261.gif) 或3≤
或3≤年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image265.gif) .
-----------------14分
.
-----------------14分
17.(本小題滿分15分)
解:(1)設(shè)方程年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image141.gif) 有實(shí)根為事件
有實(shí)根為事件年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image182.gif) .
.
數(shù)對(duì)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image268.gif) 共有
共有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image270.gif) 對(duì).
------------------2分
對(duì).
------------------2分
若方程有實(shí)根,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image272.gif) ≥
≥年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image274.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image276.gif) . -----------------4分
. -----------------4分
則使方程有實(shí)根的數(shù)對(duì)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image268.gif) 有
有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image278.gif) 共
共年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image280.gif) 對(duì).
------------------6分
對(duì).
------------------6分
所以方程有實(shí)根的概率年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image282.gif) .
------------------8分
.
------------------8分
(2)設(shè)方程年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image141.gif) 有實(shí)根為事件
有實(shí)根為事件年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image184.gif) .
.
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image285.gif) ,所以
,所以年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image287.gif) .
------------------10分
.
------------------10分
方程有實(shí)根對(duì)應(yīng)區(qū)域?yàn)?sub>年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image289.gif) ,
,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image291.gif) . -------------------12分
. -------------------12分
所以方程有實(shí)根的概率年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image293.gif) .
------------------15分
.
------------------15分
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image295.jpg) 18.(本小題滿分15分)
18.(本小題滿分15分)
解:(1)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image297.gif) ∴
∴年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image299.gif) ………………4分
………………4分
(2)過年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image301.gif) 的切線斜率
的切線斜率年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image303.gif) .
.
∴切線方程為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image305.gif) .
.
準(zhǔn)線方程為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image307.gif) . …………………8分
. …………………8分
∴年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image309.gif) .∴
.∴年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image311.gif) . ………………………………12分
. ………………………………12分
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image162.gif) 在
在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image314.gif) 單調(diào)遞增,∴
單調(diào)遞增,∴年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image316.gif) ,
,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image318.gif) .
.
∴年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image162.gif) 的取值范圍是-
的取值范圍是-年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image320.gif) .
………………………………15分
.
………………………………15分
19.(本小題滿分16分)
解:(1)設(shè)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image172.gif) 關(guān)于l的對(duì)稱點(diǎn)為
關(guān)于l的對(duì)稱點(diǎn)為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image323.gif) ,則
,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image325.gif) 且
且年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image327.gif) ,解得
,解得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image329.gif) ,
,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image331.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image333.gif) ,故直線
,故直線年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image335.gif) 的方程為
的方程為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image337.gif) .由
.由年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image339.gif) ,解得
,解得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image341.gif) .
------------------------5分
.
------------------------5分
(2)因?yàn)?sub>年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image343.gif) ,根據(jù)橢圓定義,得
,根據(jù)橢圓定義,得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image345.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image347.gif) ,所以
,所以年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image349.gif) .又
.又年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image351.gif) ,所以
,所以年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image353.gif) .所以橢圓
.所以橢圓年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image154.gif) 的方程為
的方程為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image355.gif) .
------------------------10分
.
------------------------10分
(3)假設(shè)存在兩定點(diǎn)為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image357.gif) ,使得對(duì)于橢圓上任意一點(diǎn)
,使得對(duì)于橢圓上任意一點(diǎn)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image359.gif) (除長(zhǎng)軸兩端點(diǎn))都有
(除長(zhǎng)軸兩端點(diǎn))都有年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image361.gif) (
(年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image363.gif) 為定值),即
為定值),即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image365.gif) ?
?年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image367.gif) ,將
,將年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image369.gif) 代入并整理得
代入并整理得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image371.gif) …(*).
…(*).
由題意,(*)式對(duì)任意年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image373.gif) 恒成立,所以
恒成立,所以年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image375.gif) ,
,
解之得 年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image377.gif) 或
或年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image379.gif) .
.
所以有且只有兩定點(diǎn)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image381.gif) ,使得
,使得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image383.gif) 為定值
為定值年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image385.gif) . ---------------16分
. ---------------16分
(注:若猜出年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image182.gif) 、
、年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image184.gif) 點(diǎn)為長(zhǎng)軸兩端點(diǎn)并求出定值,給3分)
點(diǎn)為長(zhǎng)軸兩端點(diǎn)并求出定值,給3分)
20.(本小題滿分16分)
解:(1)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image099.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image390.gif) .
------------------------2分
.
------------------------2分
因?yàn)?sub>年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image392.gif) ,令
,令年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image394.gif) 得
得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image396.gif) ;令
;令年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image398.gif) 得
得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image400.gif) .所以函數(shù)的增區(qū)間為
.所以函數(shù)的增區(qū)間為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image402.gif) ,減區(qū)間為
,減區(qū)間為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image404.gif) .
------------------------5分
.
------------------------5分
(2)因?yàn)?sub>年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image099.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image406.gif) ,設(shè)
,設(shè)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image408.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image192.gif) ,則
,則年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image411.gif) .----------6分
.----------6分
設(shè)切點(diǎn)為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image413.gif) ,則切線的斜率為
,則切線的斜率為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image415.gif) ,切線方程為
,切線方程為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image417.gif) 即
即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image419.gif) ,由點(diǎn)
,由點(diǎn)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image149.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image202.gif) 在切線上知
在切線上知年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image422.gif) ,化簡(jiǎn)得
,化簡(jiǎn)得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image424.gif) ,即
,即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image426.gif) .
.
所以僅可作一條切線,方程是年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image428.gif) .
------------------------9分
.
------------------------9分
(3)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image099.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image430.gif) ,
,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image392.gif) .
.
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image212.gif) 在
在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image433.gif) 上恒成立
上恒成立年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image435.gif)
年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image075.gif) 在
在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image433.gif) 上的最小值
上的最小值年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image438.gif) .--------------11分
.--------------11分
①當(dāng)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image440.gif) 時(shí),
時(shí),年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image442.gif) 在
在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image444.gif) 上單調(diào)遞減,
上單調(diào)遞減,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image075.gif) 在
在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image210.gif) 上最小值為
上最小值為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image447.gif) ,不符合題意,故舍去;
------------------------12分
,不符合題意,故舍去;
------------------------12分
②當(dāng)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image199.gif) 時(shí),令
時(shí),令年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image450.gif) 得
得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image452.gif) .
.
當(dāng)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image454.gif) 時(shí),即
時(shí),即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image456.gif) 時(shí),函數(shù)在
時(shí),函數(shù)在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image210.gif) 上遞增,
上遞增,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image075.gif) 的最小值為
的最小值為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image458.gif) ;解得
;解得年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image460.gif) .
------------------------13分
.
------------------------13分
當(dāng)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image462.gif) 時(shí),即
時(shí),即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image464.gif) 時(shí),函數(shù)在
時(shí),函數(shù)在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image210.gif) 上遞減,
上遞減,年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image075.gif) 的最小值為
的最小值為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image466.gif) ,無解;
-----------------------14分
,無解;
-----------------------14分
當(dāng)年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image468.gif) 時(shí),即
時(shí),即年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image470.gif) 時(shí),函數(shù)在
時(shí),函數(shù)在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image472.gif) 上遞減、在
上遞減、在年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image474.gif) 上遞增,所以
上遞增,所以年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image075.gif) 的最小值為
的最小值為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image476.gif) ,無解.
------------------------15分
,無解.
------------------------15分
綜上,所求年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image194.gif) 的取值范圍為
的取值范圍為年高二第一學(xué)期期末聯(lián)考數(shù)學(xué)文科試題.files/image479.gif) .
------------------------16分
.
------------------------16分
國(guó)際學(xué)校優(yōu)選 - 練習(xí)冊(cè)列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報(bào)平臺(tái) | 網(wǎng)上有害信息舉報(bào)專區(qū) | 電信詐騙舉報(bào)專區(qū) | 涉歷史虛無主義有害信息舉報(bào)專區(qū) | 涉企侵權(quán)舉報(bào)專區(qū)
違法和不良信息舉報(bào)電話:027-86699610 舉報(bào)郵箱:58377363@163.com