
題目列表(包括答案和解析)
定義在R上的任意函數(shù)f (x)都可以表示成一個奇函數(shù)g (x)和一個偶函數(shù)h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
A.g (x)=x,h (x)=lg(10x+10-x+1)
B.g (x)= ,h (x)=
,h (x)=
C.g (x)= ,h (x)=lg(10x+1)-
,h (x)=lg(10x+1)-
D.g (x)=- ,h (x)=
,h (x)=
定義在R上的任意函數(shù)f (x)都可以表示成一個奇函數(shù)g (x)和一個偶函數(shù)h (x)之和,如果f (x)=lg(10x+1),x∈R.那么
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)= ,h (x)= ,h (x)= |
C.g (x)= ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)- |
D.g (x)=- ,h (x)= ,h (x)= |
| A.g (x)=x,h (x)=lg(10x+10-x+1) |
B.g (x)=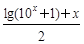 ,h (x)= ,h (x)=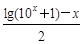 |
C.g (x)=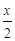 ,h (x)=lg(10x+1)- ,h (x)=lg(10x+1)-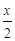 |
D.g (x)=-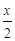 ,h (x)= ,h (x)=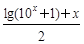 |
定義在R上的任意函數(shù)f(x)都可以表示成一個奇函數(shù)g(x)與一個偶函數(shù)h(x)的和.若f(x)=lg(10x+1),x∈R,求g(x),h(x)的解析式.
①若存在x1,x2∈R,x1<x2,使f(x1)<f(x2)成立,則函數(shù)f(x)在R上單調(diào)遞增;
②若存在x1,x2∈R,x1<x2,使f(x1)≤f(x2)成立,則函數(shù)f(x)在R上不可能單調(diào)遞減;
③若存在x2>0,對于任意x1∈R,都有f(x1)<f(x1+x2)成立,則函數(shù)f(x)在R上單調(diào)遞增;
④對任意x1,x2∈R,x1<x2,都有f(x1)≥f(x2)成立,則函數(shù)f(x)在R上單調(diào)遞減.
以上命題正確的序號是( )
A.①③ B.②③ C.②④ D.②
國際學校優(yōu)選 - 練習冊列表 - 試題列表
湖北省互聯(lián)網(wǎng)違法和不良信息舉報平臺 | 網(wǎng)上有害信息舉報專區(qū) | 電信詐騙舉報專區(qū) | 涉歷史虛無主義有害信息舉報專區(qū) | 涉企侵權舉報專區(qū)
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com