精品一区二区免费在线观看_国产精品久久久久久av福利软件_97成人精品区在线播放_国内成人精品一区

A.2k+2                       B.（2k+1）（2k+2）

C.                    D.

數(shù)列首項，前項和滿足等式（常數(shù)，……）

（1）求證：為等比數(shù)列；

（2）設(shè)數(shù)列的公比為，作數(shù)列使 （……），求數(shù)列的通項公式.

（3）設(shè)，求數(shù)列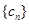的前項和.

【解析】第一問利用由得

兩式相減得

故時，

從而又  即，而

從而  故

第二問中，     又故為等比數(shù)列，通項公式為

第三問中，

兩邊同乘以

利用錯位相減法得到和。

（1）由得

兩式相減得

故時，

從而   ………………3分

又  即，而

從而  故

對任意，為常數(shù)，即為等比數(shù)列………………5分

（2）    ……………………7分

又故為等比數(shù)列，通項公式為………………9分

（3）

兩邊同乘以

………………11分

兩式相減得

方程的解可視為函數(shù)的圖像與函數(shù)的圖像交點的橫坐標(biāo). 若方程的各個實根所對應(yīng)的點()（=）均在直線的同側(cè)，則實數(shù)的取值范圍是                .