
題目列表(包括答案和解析)
4. m>2或m<-2 解析:因為f(x)=![]() 在(-1,1)內有零點,所以f(-1)f(1)<0,即(2+m)(2-m)<0,則m>2或m<-2
在(-1,1)內有零點,所以f(-1)f(1)<0,即(2+m)(2-m)<0,則m>2或m<-2
隨機變量![]() 的所有等可能取值為1,2…,n,若
的所有等可能取值為1,2…,n,若![]() ,則( )
,則( )
A. n=3 B.n=4 C. n=5 D.不能確定
5.m=-3,n=2 解析:因為![]() 的兩零點分別是1與2,所以
的兩零點分別是1與2,所以![]() ,即
,即![]() ,解得
,解得![]()
6.![]() 解析:因為
解析:因為![]() 只有一個零點,所以方程
只有一個零點,所以方程![]() 只有一個根,因此
只有一個根,因此![]() ,所以
,所以![]()
某港口海水的深度 (米)是時間
(米)是時間 (時)(
(時)( )的函數,記為:
)的函數,記為:
已知某日海水深度的數據如下:
|
|
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
|
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
經長期觀察, 的曲線可近似地看成函數
的曲線可近似地看成函數 的圖象
的圖象
(I)試根據以上數據,求出函數 的振幅、最小正周期和表達式;
的振幅、最小正周期和表達式;
(II)一般情況下,船舶航行時,船底離海底的距離為 米或
米或 米以上時認為是安全的(船舶停靠時,船底只需不碰海底即可)。某船吃水深度(船底離水面的距離)為
米以上時認為是安全的(船舶停靠時,船底只需不碰海底即可)。某船吃水深度(船底離水面的距離)為 米,如果該船希望在同一天內安全進出港,請問,它至多能在港內停留多長時間(忽略進出港所需時間)
米,如果該船希望在同一天內安全進出港,請問,它至多能在港內停留多長時間(忽略進出港所需時間)
【解析】第一問中利用三角函數的最小正周期為:
T=12 振幅:A=3,b=10,

 第二問中,該船安全進出港,需滿足:
第二問中,該船安全進出港,需滿足: 即:
即:
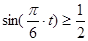 ∴
∴ 又
又  ,可解得結論為
,可解得結論為 或
或 得到。
得到。
已知遞增等差數列 滿足:
滿足: ,且
,且 成等比數列.
成等比數列.
(1)求數列 的通項公式
的通項公式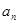 ;
;
(2)若不等式 對任意
對任意 恒成立,試猜想出實數
恒成立,試猜想出實數 的最小值,并證明.
的最小值,并證明.
【解析】本試題主要考查了數列的通項公式的運用以及數列求和的運用。第一問中,利用設數列 公差為
公差為 ,
,
由題意可知 ,即
,即 ,解得d,得到通項公式,第二問中,不等式等價于
,解得d,得到通項公式,第二問中,不等式等價于 ,利用當
,利用當 時,
時, ;當
;當 時,
時, ;而
;而 ,所以猜想,
,所以猜想, 的最小值為
的最小值為 然后加以證明即可。
然后加以證明即可。
解:(1)設數列 公差為
公差為 ,由題意可知
,由題意可知 ,即
,即 ,
,
解得 或
或 (舍去). …………3分
(舍去). …………3分
所以, . …………6分
. …………6分
(2)不等式等價于 ,
,
當 時,
時, ;當
;當 時,
時, ;
;
而 ,所以猜想,
,所以猜想, 的最小值為
的最小值為 . …………8分
. …………8分
下證不等式 對任意
對任意 恒成立.
恒成立.
方法一:數學歸納法.
當 時,
時, ,成立.
,成立.
假設當 時,不等式
時,不等式 成立,
成立,
當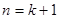 時,
時, ,
…………10分
,
…………10分
只要證  ,只要證
,只要證  ,
,
只要證  ,只要證
,只要證  ,
,
只要證  ,顯然成立.所以,對任意
,顯然成立.所以,對任意 ,不等式
,不等式 恒成立.…14分
恒成立.…14分
方法二:單調性證明.
要證 
只要證  ,
,
設數列 的通項公式
的通項公式 , …………10分
, …………10分
 , …………12分
, …………12分
所以對 ,都有
,都有 ,可知數列
,可知數列 為單調遞減數列.
為單調遞減數列.
而 ,所以
,所以 恒成立,
恒成立,
故 的最小值為
的最小值為 .
.
已知函數
(1)若函數 的圖象經過P(3,4)點,求a的值;
的圖象經過P(3,4)點,求a的值;
(2)比較 大小,并寫出比較過程;
大小,并寫出比較過程;
(3)若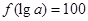 ,求a的值.
,求a的值.
【解析】本試題主要考查了指數函數的性質的運用。第一問中,因為函數 的圖象經過P(3,4)點,所以
的圖象經過P(3,4)點,所以 ,解得
,解得 ,因為
,因為 ,所以
,所以 .
.
(2)問中,對底數a進行分類討論,利用單調性求解得到。
(3)中,由 知,
知, .,指對數互化得到
.,指對數互化得到 ,,所以
,,所以 ,解得所以,
,解得所以, 或
或  .
.
解:⑴∵函數 的圖象經過
的圖象經過 ∴
∴ ,即
,即 . … 2分
. … 2分
又 ,所以
,所以 .
………… 4分
.
………… 4分
⑵當 時,
時, ;
;
當 時,
時, . ……………… 6分
. ……………… 6分
因為, ,
,
當 時,
時, 在
在 上為增函數,∵
上為增函數,∵ ,∴
,∴ .
.
即 .當
.當 時,
時, 在
在 上為減函數,
上為減函數,
∵ ,∴
,∴ .即
.即 . …………………… 8分
. …………………… 8分
⑶由 知,
知, .所以,
.所以, (或
(或 ).
).
∴ .∴
.∴ , … 10分
, … 10分
∴ 或
或
 ,所以,
,所以, 或
或  .
.
如圖,已知點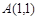 和單位圓上半部分上的動點B.
和單位圓上半部分上的動點B.
(1)若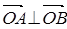 ,求向量
,求向量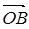 ;
;
(2)求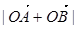 的最大值.
的最大值.
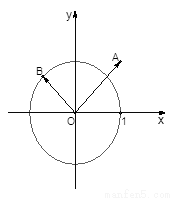
【解析】對于這樣的向量的坐標和模最值的求解,利用建立直角坐標系的方法可知。
第一問中,依題意,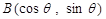 ,
,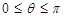
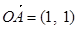 ,
,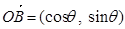
因為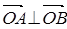 ,所以
,所以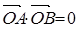 ,即
,即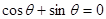 ,
,
解得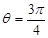 ,所以
,所以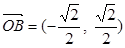
第二問中,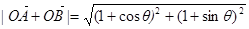 結合三角函數的性質得到最值。
結合三角函數的性質得到最值。
(1)依題意,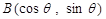 ,
,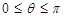 (不含1個或2個端點也對)
(不含1個或2個端點也對)
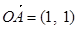 ,
,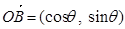 (寫出1個即可)
(寫出1個即可)
因為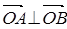 ,所以
,所以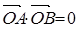 ,即
,即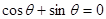 ,
,
解得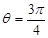 ,所以
,所以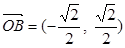 .-
.-
(2)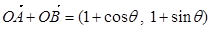 ,
,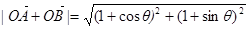
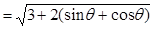
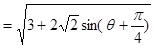 當
當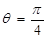 時,
時,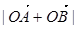 取得最大值,
取得最大值,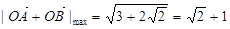
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com