
題目列表(包括答案和解析)
已知函數 =
= .
.
(Ⅰ)當 時,求不等式
時,求不等式
 ≥3的解集;
≥3的解集;
(Ⅱ) 若 ≤
≤ 的解集包含
的解集包含 ,求
,求 的取值范圍.
的取值范圍.
【命題意圖】本題主要考查含絕對值不等式的解法,是簡單題.
【解析】(Ⅰ)當 時,
時, =
= ,
,
當 ≤2時,由
≤2時,由 ≥3得
≥3得 ,解得
,解得 ≤1;
≤1;
當2< <3時,
<3時, ≥3,無解;
≥3,無解;
當 ≥3時,由
≥3時,由 ≥3得
≥3得 ≥3,解得
≥3,解得 ≥8,
≥8,
∴ ≥3的解集為{
≥3的解集為{ |
| ≤1或
≤1或 ≥8};
≥8};
(Ⅱ)  ≤
≤
 ,
,
當 ∈[1,2]時,
∈[1,2]時, =
= =2,
=2,
∴ ,有條件得
,有條件得 且
且 ,即
,即 ,
,
故滿足條件的 的取值范圍為[-3,0]
的取值范圍為[-3,0]
已知關于x的不等式|ax+2|<8的解集為(-3,5),則a=__________.
本題考查含絕對值不等式的解法.
已知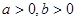 ,求證:
,求證: .
.
【解析】本試題主要是考查了不等式的證明,利用分析法進行變形化簡并證明。
(1)求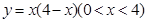 的最大值,并求
的最大值,并求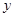 取最大值時相應的
取最大值時相應的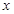 的值.
的值.
(2)若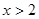 ,求
,求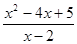 的最小值.
的最小值.
【解析】本試題主要是考查了不等式的最值思想,以及運用均值不等式求解最值的問題。
解關于x的不等式|2x+m|<x-m(x∈R).
本題考查含有絕對值不等式的解法.解題關鍵是對m進行分類討論.
湖北省互聯網違法和不良信息舉報平臺 | 網上有害信息舉報專區 | 電信詐騙舉報專區 | 涉歷史虛無主義有害信息舉報專區 | 涉企侵權舉報專區
違法和不良信息舉報電話:027-86699610 舉報郵箱:58377363@163.com