
題目列表(包括答案和解析)
設函數(shù)![]()
![]()
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(Ⅱ)記函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 有零點,求
有零點,求![]() 的取值范圍.
的取值范圍.
設函數(shù)![]()
![]() .
.
(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在
在![]() 上的最大值;
上的最大值;
(Ⅱ)記函數(shù)![]() ,若函數(shù)
,若函數(shù)![]() 有零點,求
有零點,求![]() 的取值范圍.
的取值范圍.
已知函數(shù)![]() .(Ⅰ)當
.(Ⅰ)當![]() 時,求函數(shù)
時,求函數(shù)![]() 在區(qū)間
在區(qū)間![]() 上的最大值與最小值;(Ⅱ)若存在
上的最大值與最小值;(Ⅱ)若存在![]() ,使
,使![]() ,求
,求![]() 的取值范圍.
的取值范圍.
已知函數(shù)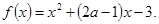
(Ⅰ)當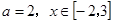 時,求函數(shù)的值域;
時,求函數(shù)的值域;
(Ⅱ)若函數(shù)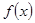 在
在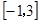 上的最大值為1,求實數(shù)a的值.
上的最大值為1,求實數(shù)a的值.
設函數(shù)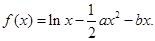
(Ⅰ)當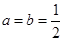 時,求
時,求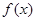 的最大值;
的最大值;
(Ⅱ)令 ,(
,(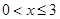 ),其圖象上任意一點
),其圖象上任意一點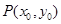 處切線的斜率
處切線的斜率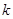 ≤
≤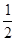 恒成立,求實數(shù)
恒成立,求實數(shù)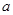 的取值范圍;
的取值范圍;
(Ⅲ)當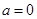 ,
, ,方程
,方程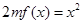 有唯一實數(shù)解,求正數(shù)
有唯一實數(shù)解,求正數(shù) 的值.
的值.
一、選擇題:本大題考查基本概念和基本運算.每小題5分,滿分60分.
1.A 2.C 3.C 4.B 5.C 6.D7.A 8.D 9.B 10.B
11.A 12.C
二、填空題:13、4 14.數(shù)學(文).files/image205.gif) 15.
15.數(shù)學(文).files/image207.gif) 16.
16.數(shù)學(文).files/image207.gif)
三、解答題:
17.解:f(x)=a(cosx+1+sinx)+b=數(shù)學(文).files/image210.gif) (2分)
(2分)
(1)當a=1時,f(x)= 數(shù)學(文).files/image212.gif) ,
,
當數(shù)學(文).files/image214.gif) 時,f(x)是增函數(shù),所以f(x)的單調遞增區(qū)間為
時,f(x)是增函數(shù),所以f(x)的單調遞增區(qū)間為數(shù)學(文).files/image216.gif) (6分)
(6分)
(2)由數(shù)學(文).files/image218.gif) 得
得數(shù)學(文).files/image220.gif) ,∴
,∴數(shù)學(文).files/image222.gif)
∴當sin(x+數(shù)學(文).files/image224.gif) )=1時,f(x)取最小值3,即
)=1時,f(x)取最小值3,即數(shù)學(文).files/image226.gif) ,
,
當sin(x+數(shù)學(文).files/image224.gif) )=
)=數(shù)學(文).files/image228.gif) 時,f(x)取最大值4,即b=4.
(10分)
時,f(x)取最大值4,即b=4.
(10分)
將b=4 代入上式得數(shù)學(文).files/image230.gif) ,故a+b=
,故a+b=數(shù)學(文).files/image232.gif) (12分)
(12分)
18.解:設甲、乙兩條船到達的時刻分別為x,y.則數(shù)學(文).files/image234.gif)
若甲先到,則乙必須晚1小時以上到達,即數(shù)學(文).files/image236.gif)
若乙先到達,則甲必須晚2小時以上到達,即數(shù)學(文).files/image238.gif)
作圖,(略).利用面積比可算出概率為數(shù)學(文).files/image240.gif) .
.
19.
解:(I)如圖所示, 連結數(shù)學(文).files/image242.gif) 由
由數(shù)學(文).files/image145.gif) 是菱形且
是菱形且數(shù)學(文).files/image147.gif) 知,
知,
數(shù)學(文).files/image244.gif) 是等邊三角形. 因為E是CD的中點,所以
是等邊三角形. 因為E是CD的中點,所以
數(shù)學(文).files/image246.gif) 又
又數(shù)學(文).files/image248.gif) 所以
所以數(shù)學(文).files/image250.gif)
又因為PA數(shù)學(文).files/image149.gif) 平面ABCD,
平面ABCD,數(shù)學(文).files/image252.gif) 平面ABCD,
平面ABCD,
所以數(shù)學(文).files/image254.gif) 而
而數(shù)學(文).files/image256.gif) 因此
因此 數(shù)學(文).files/image258.gif) 平面PAB.
平面PAB.
又數(shù)學(文).files/image252.gif) 平面PBE,所以平面PBE
平面PBE,所以平面PBE數(shù)學(文).files/image149.gif) 平面PAB.
平面PAB.
(II)由(I)知,數(shù)學(文).files/image258.gif) 平面PAB,
平面PAB, 數(shù)學(文).files/image260.gif) 平面PAB, 所以
平面PAB, 所以數(shù)學(文).files/image262.gif)
又數(shù)學(文).files/image264.gif) 所以
所以數(shù)學(文).files/image266.gif) 是二面角
是二面角數(shù)學(文).files/image268.gif) 的平面角.
的平面角.
在數(shù)學(文).files/image270.gif) 中,
中, 數(shù)學(文).files/image272.gif) .
.
故二面角數(shù)學(文).files/image268.gif) 的大小為
的大小為數(shù)學(文).files/image274.gif)
20.解:
(1)數(shù)學(文).files/image276.gif)
數(shù)學(文).files/image278.gif) .
.
數(shù)學(文).files/image280.gif) 上是增函數(shù).
上是增函數(shù).
(2)數(shù)學(文).files/image282.gif)
(i)
當數(shù)學(文).files/image284.gif)
數(shù)學(文).files/image286.gif)
數(shù)學(文).files/image288.gif) 的單調遞增區(qū)間是
的單調遞增區(qū)間是數(shù)學(文).files/image290.gif)
(ii)
當數(shù)學(文).files/image292.gif)
當數(shù)學(文).files/image294.gif)
數(shù)學(文).files/image295.gif) 的單調遞增區(qū)間是
的單調遞增區(qū)間是數(shù)學(文).files/image297.gif) 單調遞減區(qū)間是
單調遞減區(qū)間是數(shù)學(文).files/image299.gif) . 所以,
. 所以,數(shù)學(文).files/image300.gif) 的單調遞增區(qū)間是
的單調遞增區(qū)間是數(shù)學(文).files/image302.gif) 單調遞減區(qū)間是
單調遞減區(qū)間是數(shù)學(文).files/image303.gif) .
.
由上知,當x=1時,f(x)取得極大值f(1)=2
又b>1,由2=b3-3b,解得b=2.
所以,數(shù)學(文).files/image305.gif) 時取得最大值f(1)=2.
時取得最大值f(1)=2.
當數(shù)學(文).files/image307.gif) 時取得最大值
時取得最大值數(shù)學(文).files/image309.gif) .
.